This question investigates the effect of extending the data set with zero-padding & of the appropriate time in the workflow to apply a window function. To get finer resolution in the frequency domain, the original signal can be zero-padded, that is, zeros appended to the end of the time-domain signal. 

Consider an input signal consisting of a strong 100 Hz sine wave & a weak 184.25 Hz signal & some weak noise. This is given by:

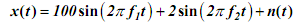
with f₁= 100hz  & f₂ = 184.25hz the noise n(t) is a Gaussian distributed random signal with zero mean & unity variance.

This signal is sampled at a frequency of 1 kHz and 64 samples are available. Derive the PSD of the data set & plot on a decibel scale as specified below:

a)  using the data set without zero padding.

b)  using the data set extended to 512 points by zero-padding.

c)  using the extended data set modified by a Hamming window.

d)  using the original 64 point data set modified by a Hamming window but then extended to 512 points by zero-padding. 

You should therefore produce 4 sets of graphs corresponding to questions a-d - each set consisting of a magnitude-time & db-frequency pair.

Comment on your results as to which process 'pulls out' the best results from the FFT process.

Repeat this question using other common windows (von Hann, Blackman, Blackman-Harris, Nuttall) and using different zero-padding lengths.

What are the overall conclusions from this exercise?