Gravitational Field inside a Spherical Shell

In this problem we prove that the gravitational field inside a thin spherical shell of finitemass is zero. By extension, the field inside a thick shellwhoseinner and outer radii are finite is also zero. In this gure, R is the radius ofthe shell andMits mass. The mass per unit area is σ = M/S where S is the surface area. An object of mass m is located at point p, which is at distancer from the center of the sphere.

An element of mass is given by dM = σ × 2π R × R sin θ dθ, which corresponds to the ring on the surface. If the gravitational force along the lines is resolved into inline and perpendicular components, we find that the perpendicular components (Rsin θ) cancel and only the inline (Rcos θ) components contribute. Therefore the acceleration due to a gravitational element is:

da =GdM/s²cos φ.

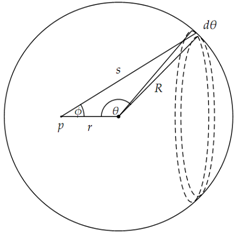
Substituting for dM as well as integrating over the surface

We have

a = σ2πG∫^π_θ=0 (cos φ sin θ/s²)dθ.

Currently we express s and φ in terms of θ.

s²= R²+ r²- 2R r cos θ

Using the law of cosines. Differentiating,                         

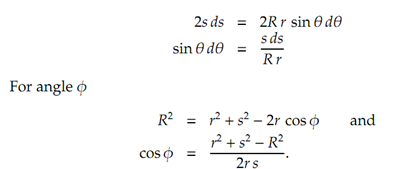
We are able to now make the necessary substitutions, mindful that changing the variable of integration changes the limits.

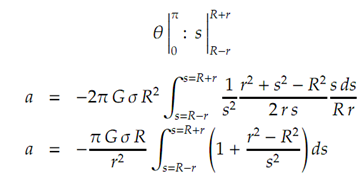
Now σ = M/4π R² consequently

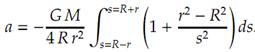
Integrating,

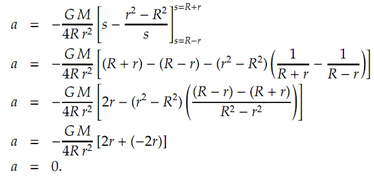
Thus the acceleration due to gravity at any point inside a thin spherical shell is identically zero! There are other simpler approaches to find this solution. For example Gauss' Law immediately yields the same result.