Graph for the Sequence

First we wish to think about the term graphing a sequence. To graph the sequence {a_n} we plot the points {n, a_n} as n ranges over every possible values on a graph. For example, let's graph the sequence {n+1 / n²}^∞ _{n =1}. The 1^st few important points on the graph are,

 (1,2) , (2, ¾ ) , (3, 4/9) , (4, 5/16) , (5, 6/25), ....

After that the graph, for the first 30 terms of the sequence is as follow:

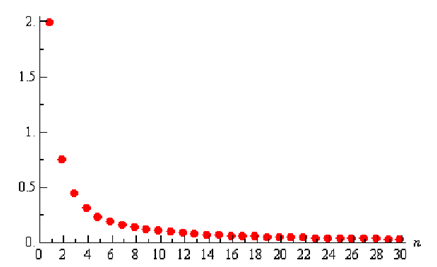
This graph leads us to a major idea regarding to the sequences.  Note: As n increases the sequence terms in our sequence, in this example, get closer and closer to zero.  After that we say that zero is the limit (or sometimes the limiting value) of the sequence and write,

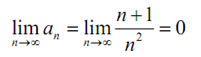
This note should look well known to you.  It is similar notation we used while we talked about the limit of a function.  Actually, if you remind, we said previous that we could think of sequences as functions in some way and thus this notation shouldn't be also surprising.