Fundamentals of Structured Product Engineering

1. (a) Let r_m denote the m month swap rate (or Libor rate). Subsequently the 3 × n month forward rate f_{(3×n) i}s calculated therefore

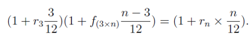
The discount curve is calculated therefore the n- month discount rate B(t₀, t_n) is

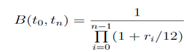
(b) The 24 × n month forward rate f_(3×n) is calculated therefore:

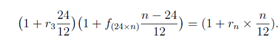
(c) The components for this memo is a discount curve a 2-year forward curve a market for CMS swaps and Bermuda swaptions since the note is callable.

(d) Let cms^j,k_i denote j-year CMS purchased for k years evaluated at the i-th year. Let c_t0 be the premium for a 2-year Bermuda swaption.

Compute R₁ = L₀ +α₀ where L₀ is the current 1-year Libor rate and α₀ is calculated as

c_t0 = α₀ + B(t₀, t₁)α₀ + B(t₀, t₂)α₀.

Year 2 coupon is: α₁(cms₂,³² )+L₀+α₀. We know cms₂,³² and therefore α₁ is calculated by equating:

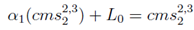
giving α₁ = 1- L₀/cms₂^,32. Likewise α₂ is calculated from

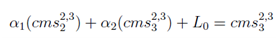
giving α₂ = 1- cms₂,³²/cms₂,³³.

(e) The components for this memo is a discount curve a 3-year and a 2-year forward curve a market for CMS swaps and Bermuda swaptions (since the note is callable).

(f) Let's c_t0 be the premium for a 2-year Bermuda swaption. Compute R₁ = L₀ +α₀, where L₀ is the current 1-year Libor rate and α₀ is calculated as

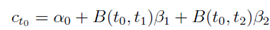
At this point c_t0,B(t₀, t₁),B(t₀, t₂) are known and the rest α₀, β₁, β₂ has to be determined from that. α is computed as α = (cms^3,3₀-cms^2,3₀)/s³₀where s30is the 3-year swap rate.

(g) β₁ = β₂ can be chosen appropriately to satisfy c_t0 = α₀+B(t₀, t₁)β₁ +B(t₀, t₂)β₂.

2. (a) The note can be engineered therefore

• 1-year Libor deposit.

• Contract into a receiver interest rate swap paying Libor and getting 5.23%.

• Buy digital cap (for Libor > 6.13%) as well as digital floor (for Libor > 6.13%).

• Pay CMS10 for first 2 years as well as 8 × CMS10 for the next three years.

• Receive CMS30 for first 2 years as well as 8×CMS30 for the next three years.

(b) An investor who anticipate the yield curve to steepen in the long run and expects Libor to remain quite high would demand this product. He or She would expect Libor to increase and also the CMS spread to increase leading to an increase in the difference CMS30 -CMS10.