Functions of Several Variables - Three Dimensional Space

In this part we want to go over a few of the basic ideas about functions of much more than one variable.

Very first, keep in mind that graphs of functions of two variables, z = f (x, y) are surfaces in three dimensional (3D) space. For instance here is the graph of z = 2x² + 2y² -4.

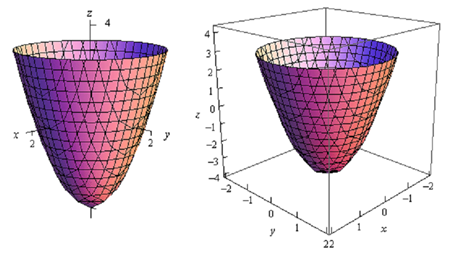
This is an elliptic parabaloid and is an instance of a quadric surface. We saw so many of these in the earlier section. We will be seeing quadric surfaces quite regularly later.

Other common graph that we will be seeing quite a bit in this course is the graph of a plane.  We comprise a convention for graphing planes which will make them a slightly easier to graph and hopefully visualize.

Remind that the equation of a plane is illustrated by

ax + by + cz = d

or if we solve this equation for z we can write it in terms of function notation. This provides,

f (x, y) = Ax + By + D

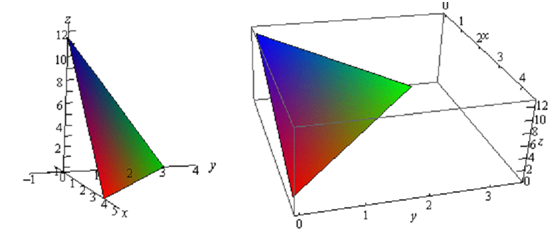
To graph a plane we will usually find the intersection points along with the three axes and then graph the triangle which connects those three points. This triangle will be a part of the plane and will provide us a fairly decent thought on what the plane itself should act like.  For instance let's graph the plane illustrated by,

f (x, y) = 12 - 3x - 4 y

For the aim of graphing this it would possibly be easier to write this as,

 z = 12 - 3x - 4 y                                ⇒         3x + 4 y + z = 12

Here now, each of the intersection points along with the three main coordinate axes is described by the fact that two of the coordinates are zero.  Example for this, the intersection with the z-axis is illustrated by x = y = 0.  Thus, the three intersection points are,

x - axis : (4, 0, 0)

y - axis : (0, 3, 0)

z - axis : (0, 0,12)

Below is the graph of the plane.

Now here, to extend this out, graphs of functions of the type w = f (x, y, z) would be four dimensional surfaces.  Actually we cannot graph them, although it does not hurt to point this out. We next wish to talk about the domains of functions of much more than one variable.  Remind that domains of functions of a single variable, y = f (x), contained all the values of x that we could plug into the function and get back a real number. At present, if we think about it, the meaning of this is that the domain of a function of a single variable is an interval (or intervals) of values from the number line or one dimensional space.

The domain of functions of two variables that are, z = f (x, y), are regions from two dimensional space and contain all the coordinate pairs, (x, y) , that we could plug into the function and obtain back a real number.