Flight of the Bumblebee
Railroad train Ta leaves station A at a uniform speed of 30mph toward station B. Train Tb leaves station B at a uniform speed of 20mph toward station A. The stations are 50 miles apart, When Ta starts, and a bumblebee which had been resting on its front begins flying toward Tb at 60mph. When the bee strikes Tb it reverses direction and heads back to Ta. It carry on these alternations until the trains collide.
How distant does the bee travel?
This problem is simple but instructive, because it invites the unwary to try a variety of unnecessarily complicated solution techniques. The essential point is that the trains travel 50 miles and with the speeds given, the trip will take 1 hour. However the bee travels at 60mph so the bee travels 60 miles. This interesting problem isn't likely to be posed in your favourite physics text but it illustrates the value of mathematical concepts in physics and a certain rubber ball has been found to exhibit a coefficient of restitution, c = 0.9. This coefficient is a ratio of an objects velocity just after and just before a collision (bounce). Then c = v1/v0 where v0 is the velocity before the bounce as well as v1 is the rebound velocity. From the kinematics equation,
v =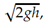 
for motion under the influence of gravity we find
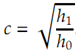
The ball will be felled on a hard surface and the following problems will be solved a) what total distances will the ball travel before it stops? And b) what is the total time the ball is in motion?
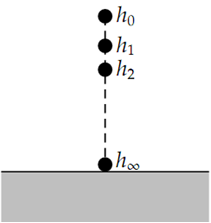
Let the preliminary height from which the ball is dropped be h0. After that the peak height on the first bounce is h1 = c2 h0. Likewise the peak height on the second bounce is h2 = c2 h1 = c4 h0. The entirety distance covered by the bouncing ball is then
d = h0 + 2c2h0 + 2c4 h0 + 2c6 h0 + ......
d = h0 + 2c2h0(1 + c2+ c4+ ....... )