Find the volume of a cylinder of radius r and height h.
Solution : Here, as we mentioned before starting this illustration we actually don't require using an integral to get this volume, but it is a good illustration to exemplify the method we'll require to use for these kinds of problems.
We will start off with the diagram of the cylinder below.
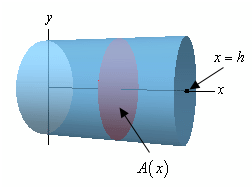
We will center the cylinder on the x-axis and the cylinder will begin at x = 0 and end at x = h as demonstrated. Remember that we are only choosing this exact set up to find an integral in terms of x and to create the limits nice to deal along with. There are various other orientations which we could use.
What we require now is to find a formula for the cross-sectional area at any x. During this case the cross- sectional area is constant and it will be a disk of radius r. Thus, for any x we'll have the subsequent cross-sectional area,
A (x)= pr2
After that the limits for the integral will be as 0 ≤ x ≤ h as i.e. the range of x wherein the cylinder lives. Now there is the integral for the volume,
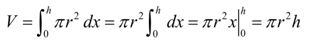
Therefore, we find the expected formula.
And, recall we are using r to classify the radius of the cylinder. Whereas r can clearly take various values this will never change once we begin the problem. Cylinder's radius does not change in the middle of a problem and therefore as we move along the center of the cylinder that is the x- axis, r is a fixed number and was not change. Conversely, this is a constant which will not change when we change the x. Thus, as we integrated with respect to x the r will be a constant as much as the integral is associated. The r can after that be pulled out of the integral as demonstrated, though that's not needed, we just did this to make the point. At this point we are only integrating dx and we identify how to do that.
While we evaluate the integral keep in mind that the restrictions are x values and therefore we plug in the x and NOT the r. Again, keep in mind that r is only a letter which is being used to represent the radius of the cylinder and, once we start the integration, is assumed to be a fixed constant.
Since observed before we started this illustration if you are having trouble along with the r just think of what you would do whether there was a 2 there in place of an r. In this problem, as we're integrating with respect to x, both the 2 and the r will behave in similar way. Note though that you must NEVER really replace the r with a 2 as that WILL guide to a wrong answer. You must just think of what you'd do IF the r was 2.
Therefore, to work these problems we will first require finding a sketch of the solid along with a set of x and y axes to assist us notice what's going on. At the extremely least we will require the sketch to find the limits of the integral, but we will frequently require this to see just what the cross-sectional area really is. Once we have the draw we'll require to find out a formula for the cross-sectional area and after that do the integral.