Illustration:  Find the solution to the subsequent IVP.

ty' + 2y = t² - t + 1,      y(1) = ½

Solution:

Initially divide via the t to find the differential equation in the accurate form.

y' + (2/t) Y = t - 1 + 1/t

Currently let's find the integrating factor, µ(t):

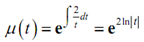
Currently, we require to simplify µ(t). Although, we can't utilize (11) as which needs a coefficient of one in front of the logarithm.  Thus, recall as

In x^r = r In x

And rewrite the integrating factor in a form which will permit us to simplify this.

µ(t) = e ^2In|t| = e^In|t|2 = |t|² = t²

We were capable to drop the absolute value bars here as we were squaring the t, but frequently they can't be dropped therefore be careful along with them and don't drop them unless you identify that you can. Frequently the absolute value bars must continue

Here, multiply the rewritten differential equation but remember that we can't utilize the original differential equation here, through the integrating factor.

(t²y)' = t³ - t² + t

Integrate both sides and resolve for the solution.

t²y = ∫t³ - t² + t dt

= ¼t⁴ - ? t³ + t dt

 y(t) = ¼t² - ? t³+ ½ + c/t²

At last, apply the initial condition to find the value of c.

½ = y(1) = ¼ - 1/3 + ½ + c ⇒ c= 1/12

The solution is afterward,

y(t) = ¼t² - ? t³+ ½ + 1/12t²

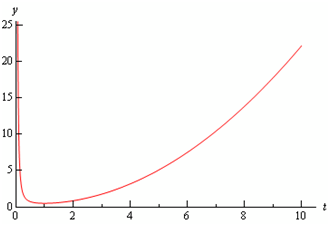
Now is a plot of the solution.