Question. Consider the triangular laminar D for given b and h shown below.
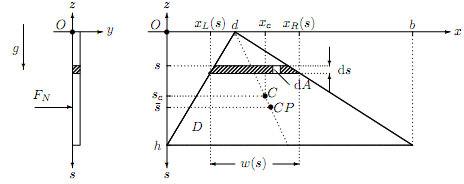
(a) Find xL(s) and xR(s), the left and right ends of the elementary strip, of thickness ds, a distance s from the x-axis. Hence gives its width w(s) and the corresponding form for1/2 [xR(s) + xL(s)].
(b) Find, by direct integration, the area, A, of the lamina. Note we can regard the lamina as a rectangle from which two right-angled triangles are removed.
(c) Find, by direct integration, the first moments of area, As|O, Ax|o , of the laminar. Hence find the position (xc; sc) of the centroid C relative to O.
(d) Find, by direct integration, the second moments of area, Ass|O ; Axs|O of the laminar. Hence, using the parallel axis theorem, obtain Ass|C and Axs|C.
(e) Suppose the triangular lamina is part of a vertical wall that separates fluid of density ½ from air at atmospheric pressure, p0. Also gravity, of acceleration g, acts in the downward vertical s-direction with the horizontal x-axis (s = 0) lying a depth s1 below the free surface. Find (i) the (resultant) hydrostatic force FN(s1) acting on the lamina. (ii) the total moments of hydrostatic force Ms and Mx about the x and s-axes.
(iii) the position (¹ x; ¹ s), of the centre of pressure CP relative to the origin O.
(iv) Show that the centroid and centre of pressure lie on the same line