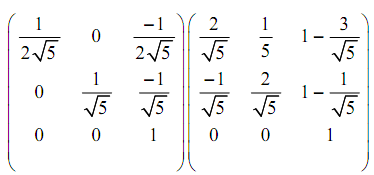Illustration: Find the normalization transformation N that uses the rectangle W (1, 1), X (5, 3), Y (4, 5) and Z (0, 3) as a window and also the normalized device screen like the viewport.

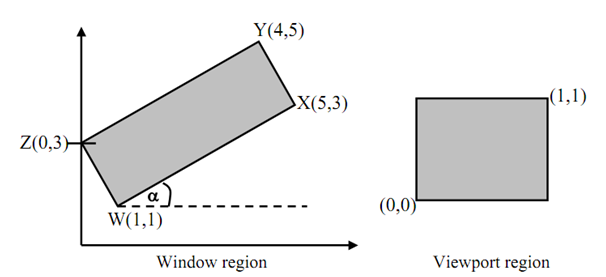
Figure: Example Transformations

Currently, we observe that the window edges are not parallel to the coordinate axes. Consequently we will first rotate the window regarding W hence it is aligned along with the axes.

Now, tan α= (3 -1)/(5-1) = 1/2

⇒ Sin α =    1 /√5;   Cos α = 2/√5

Now, we are rotating the rectangle in clockwise direction. Consequently α is negative which is, - α.

The rotation matrix about W (1, 1):

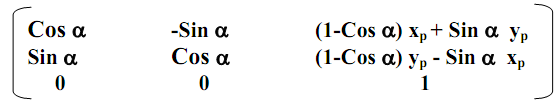
[T_R.θ]_W =

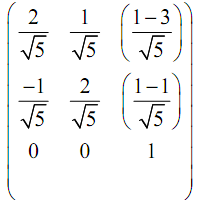
The x extent of the rotated window is the length of WX:

√(4² + 2²) = 2√5

As same, the y extent is length of WZ that is,

√ (1² + 2²) =   √5

For scaling the rotated window to the normalized viewport we calculate s_x and s_y as,

 s_x = (viewport x extent)/(window x extent)= 1/2√5

s_y = (viewport y  extent)/(window y extent) =   1/√5

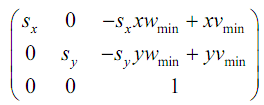
As in expression (1), the common form of transformation matrix showing mapping of a window to a viewport:

[T] =

Within this problem [T] may be termed as N as this is a case of normalization transformation with,

xw_min = 1                        xv_min = 0

yw_min = 1                        yv_min = 0

 s_x = 1/2√5      

 s_y =  1/√5

Via substituting the above values in [T] which is N:

N =

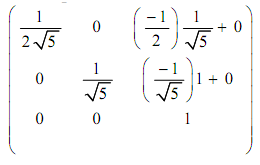
Here, we compose the rotation and transformation N to determine the needed viewing transformation NR.

 N_R = N [T_R.θ]_W =