What is required: This assignment is to be resolved using Maple. You are to upload a single Maple worksheet with file name FamilynameFirstname.mw (e.g., CarrElliot.mw), using the Assignment Upload Page available under the main MAB312 Blackboard Assessment page. Please include your full name and student number in your Maple worksheet. Your worksheet should be documented thoroughly with comments, describing your method at each step in the solution.

Question

1. As of 2012, the population of Brisbane, Sydney and Melbourne is 2,074,222, 4,627,345 and 4,137,432, respectively. It is found that each year 5% of the residents of Brisbane move to Sydney, and 5% move to Melbourne. Of the residents of Sydney, 15% move to Brisbane and 10% move to Melbourne. And of the residents of Melbourne, 10% move to Brisbane and 5% move to Sydney. Neglecting other factors (e.g., births, deaths, immigration) and assuming that the remaining 90% of Brisbane residents, 75% of Sydney residents and 85% of Melbourne residents do not move, the population in each city k years after 2012 is given by

 x(k) = Ax(k-1), k =1,2,...

where the first, second and third entry of x corresponds to the population of Brisbane, Sydney and Melbourne, respectively; 

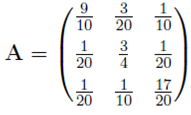
and x(0) = (2074222; 4627345; 4137432).

(a) Prove that x(k) = Akx(0).

(b) Show all working (do NOT use the Maple command Eigenvectors) in Maple to exhibit the diagonalisation of A and state the algebraic and geometric multiplicities of each eigenvalue .

(c) Use the diagonalisation of A in (b) to find the population of Brisbane, Sydney and Melbourne in 2020. Round your answers to the nearest integer.

(d) Use the diagonalisation of A to find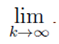

(e) Use the result in (d) to determine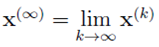 , that is, the long

term populations of each city. Further verify that (λmax, x(∞) is an

eigenpair of A, where λmax is the eigenvalue of largest magnitude.

2. Let

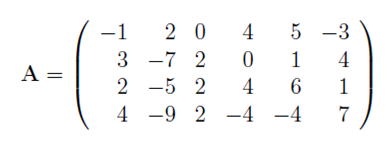
CCA

(a) Find bases for the four fundamental subspaces of A and show all working. You are to use the Maple command RowOperation (look it up in the help menu) to perform all steps in the row reduction of the appropriate matrix to row echelon form (do NOT use Maple's GaussianElimination command).

(b) What constraint(s) must be placed on an arbitrary vector b 2 R4×1, such that the nonhomogeneous linear system Ax = b is consistent?

(c) Determine if b = (7;-1; 10;-4)T satisfies the constraint(s) found in (b) and if it does, establish the general solution to Ax = b.