Solve the subsequent IVP and find the interval of validity for the solution

xyy' + 4x² + y² = 0,       y(2) = -7,          x > 0

Solution:

Let's first divide on both sides by x² to rewrite the differential equation as given,

(y/x)y' = -4 - (y²/x²)= - 4 - (y/x)²

Here, it is not in the officially exact form as we have listed above, though we can see that everywhere the variables are listed they put in an appearance as the ratio, y/x and thus this is truly as far as we require to go. Therefore, let's plug the substitution in this form of the differential equation to find,

n (n+ x n') = - 4 - n²

Subsequently, rewrite the differential equation to determine everything separated out.

n x n' = - 4 - 2n²

x n' = - (4 + 2n²)/ n

n/(4 + 2n²) dv = - (1/x) dx

Integrating on both sides we find,

¼ In (4 2n²) = - In (x) + c

We require doing a little rewriting using fundamental logarithm properties in order to be capable to easily solve this for n.

In (4 2n²)^¼ = In (x)^-1 + c

Then exponentiates on both sides and do a little rewriting,

(4 + 2n²)^¼ 

= e^In(x)-1 + c

= 

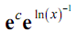
= c/x

Remember that as c is an unknown constant so next is e^c and so we may also just call this c as we did above.

At last, let's solve for v and after that plug the substitution back in and we'll play a little fast and loose along with constants again.

4 + 2n² = c⁴/x⁴ = c/x⁴

n² = ½ ((c/x⁴)- 4)

y²/x² = ½ ((c - x⁴)/x⁴)

y² = ½ x² ((c - x⁴)/x⁴)

y² = (c - x⁴)/2x²

At this point this would probably be best to go in front and apply the initial condition. Doing this gives as,

49 = (c- 4(16))/(2(4))

⇒ c = 456

Remember that we could have also transformed the original initial condition in one in terms of v and after that applied it upon solving the separable differential equation. Under this case though, it was probably a little easier to do this in terms of y provided all the logarithms in the solution to the separable differential equation.

At last, plug in c and solve for y to find:

y² = (228 - 2x⁴) /x²

⇒ Y(x) = + √((228 - 2x⁴) /x²)

Here the initial condition tells us that the "-" should be the correct sign and thus the actual solution is as,

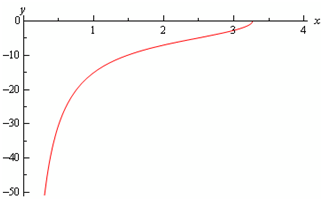
y(x) = - √((228 - 2x⁴) /x²)

For the interval of validity we can notice that we need to ignore x = 0 and since we can't allow negative numbers in the square root we also want to need,

228 - 2x⁴ > 0

x⁴ < 114 ⇒ - 3.2676 < x< 3.2676

Therefore, we have two possible intervals of validity as:

- 3.2676 < x < 0,                   x < 0< 3.2676

And the initial condition tells us that this should be 0 < x ≤ 3.2676

The graph of the solution is as: