Solve the subsequent IVP and find the interval of validity for the solution.

y' + (4/x) y = x³ y²,       y(2) = - 1,  x > 0

Solution

Thus, the first thing that we require to do is get this into the "proper" form and it means dividing everything via y².  Doing this provides,

y^-2 y' + (4/x) y^-1 = x³

The derivative and substitution that we'll require here is as:

n = y^-1,                                                n' = -y^-2y'

With this type of substitution the differential equation turns into:

- n '+ (4/x ) n = x³

Therefore as noted above it is a linear differential equation which we know how to resolve. We'll do the details on such one and after that for the rest of the illustrations in this section we will leave the details for you to fill in. If you require a refresher on solving linear differential equations so go back to which section for a rapid review.

There is the solution to this differential equation.

n '- (4/x ) n = - x³        ⇒         µ(x) = e^{∫-(4/x )dx} = e^-4In|x| = x^-4

∫(x^-4n)' dx = ∫-x^-1dx       

x⁴n = - In|x| + c          ⇒         n (x) = cx⁴ - x⁴ In x

Remember that we dropped the absolute value bars upon the x in the logarithm due to the assumption that is x >0.

Now we require determining the constant of integration. It can be done in one of two methods. We can change the solution above in a solution in terms of y and after that use the original initial condition or we can change the initial condition into an initial condition in terms of v and then use that. Since we'll need to convert the solution to y's finally anyway and this won't add that a lot work in we'll do this that way.

Therefore, to get the solution in terms of y all we require to do is plug the substitution back in.  Doing it gives:

y^-1 = x⁴ (c - In x)

We can solve for y at this point and after that apply the initial condition or apply the initial condition and after that solve for y. We'll commonly do this with the later approach thus let's apply the initial condition to find:

(-1)^-1 = c2⁴ - 2⁴ In 2      ⇒         c= In 2 - 1/16

Plugging in for c and solving for y provides:

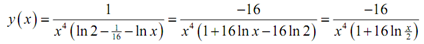
Remember that we did a little simplification into the solution. It will assists with determining the interval of validity.

Before determining the interval of validity though, we mentioned above which we could convert the original initial condition in an initial condition for n. Let's briefly talk regarding how to do such. To do that all we need to do is plug x = 2 in the substitution and after that use the original initial condition. Doing this provides,

n (2) = y^-1(2) = (-1)^-1 = -1

Thus in this case we found the same value for v which we had for y. Do not expect that to occur in general if you selected to do the problems in this way.

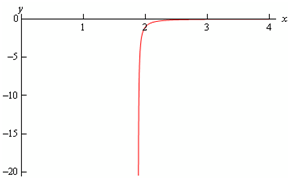
Okay, let's now determine the interval of validity for the solution. Initially we already identify that x > 0 and it implies that we'll avoid the problems of having logarithms of negative numbers and division through zero at x = 0. Hence, all that we need to worry regarding to then is division by zero in the next term and this will occur where,

1 + 16 In x/2 = 0

⇒ In x/2 = -1/16

⇒ x/2 = e ^-1/16

⇒ x = 2 e ^-1/16

≈ 1.8788

The two possible intervals of validity are after that

0 < x < 2 e ^-1/16

 2 e ^-1/16 < x < ∞

And as the second one contains the initial condition we identify that the interval of validity is so,

2 e ^-1/16 < x < ∞

Now there is a graph of the solution.