Two people are 50 feet separately.  One of them begin walking north at rate so that the angle illustrated in the diagram below is changing at constant rate of 0.01 rad/min. At what rate is distance among the two people changing when θ = 0.5 radians?

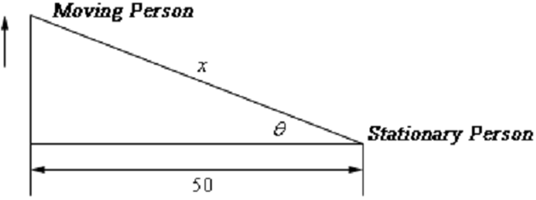
Solution : This example is not as difficult as it may at first appear. Let's call the distance among them at any instance in time x as noted above. Then we can associate all the known quantities by one of two trig formulas.

                      cos θ = 50 /x                               sec θ =  x /50

We desire to find x′ and we could determine x if we needed to at the point in question by using cosine since we also know the angle at that instance in time.  Though, if we utilize the second formula we won't have to know x as you'll illustrates.  Thus, let's differentiate that formula.

                                                sec θ tan θ θ ′ = x′ /50

As noted, there are no x's in this formula.  We desire to determine x′ & we know that θ = 0.5

and θ ′ = 0.01 . Thus, just plug in and solve.

 (50) (0.01) sec (0.5) tan (0.5) = x′      ⇒            x′ = 0.311254 ft / min

Thus far we we've illustrated three related rates problems.  Whereas each one was worked in a very distinct manner the procedure was essentially the similar in each. In each of the problem we recognized what we were given and what we desired to find.  We next wrote down a relationship among all the several quantities and utilized implicit differentiation to arrive at a relationship among the several derivatives in the problem.  At last, we plugged into the equation to determine the value we were after.

Thus, in a general sense each of the problems was worked in pretty much the similar manner. The only real difference among them was coming up with the relationship among the known and unknown

quantities. This is frequently the hardest part of the problem.  In several problems the best way to come up along with the relationship is to sketch a diagram which shows the situation. This frequently seems like a silly step, however can make all the difference in whether we can determine the relationship or not.

Let's work on another problem which uses some different ideas and illustrates some different kinds of things which can show up in related rates problems.