Two cars start out at the similar point.  One car starts out moving north at 25 mph. later on two hours the second car starts moving east at 20 mph.  How long after the first car starts moving does it take for the two cars to be 300 miles apart?

Solution

We'll start off by assuming t be the amount of time which is the first car; let's call it car A, travels.  As the second car, let's call that car B, starts out two hours later on then we know that it will travel for t - 2 hours.

Now, we know that the distance traveled through an object (or car since that's what we're dealing along with here) is its speed times time traveled.  Thus we have the following distances traveled for each of car.

Distance of car A: 25t

Distance of car B: 20 (t - 2)

At this instance a quick sketch of the condition is probably in order thus we can see just what is going on.  In the sketch we will suppose that the two cars have traveled long adequate so that they are 300 miles apart.

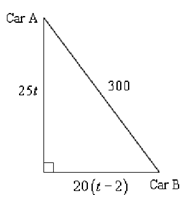
Thus, we have a right triangle here. That means that we can employ the Pythagorean Theorem to say,

                                              ( 25t )²  + (20 (t - 2))²  + (300)²

It is a quadratic equation, although it is going to require some fairly heavy simplification before we can solve it thus let's do that.

625t ² +( 20t - 40)²  =90000

625t ² + 400t ² -1600t + 1600 = 90000

1025t ² -1600t - 88400 =0

 Now, here the coefficients are quite large, although that is just something that will occur fairly frequently with these problems thus don't worry regarding that.  By using the quadratic formula (and simplifying that answer) gives,

               t =(1600 ±√365000000)/2050 = (1600±1000√365)/2050 = (32±20±√365)/41

Again, we contain two solutions & we're going to require determining which one is the correct one, so let's convert them to decimals.

t = (32 + 20 √ 365 )/41'= 10.09998 and t = (32 - 20 √ 365 )/41= -8.539011

As with the earlier example the negative answer just doesn't make any sense.  Thus, it looks like the car A traveled for 10.09998 hours while they were finally 300 miles apart.

Also, although the problem didn't ask for it, another car will have traveled for 8.09998 hours before they are 300 miles away from each other.