Find out the volume of the solid obtained by rotating the region bounded by y = (x -1) ( x - 3)² and the x-axis about the y-axis.

Solution

Let's first graph the bounded region & solid. Note as well that the bounded region here is the shaded portion illustrated. The curve is extended out a little past it for illustrating what the curve looks like.

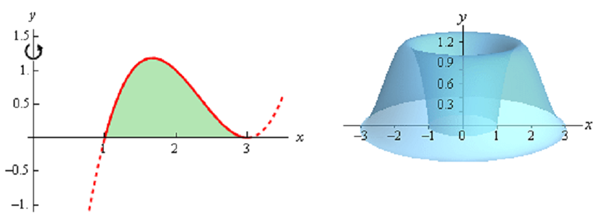
Therefore, basically we've got something that's roughly doughnut shaped.  If we were to utilize rings on this solid here is what a typical ring would look like.

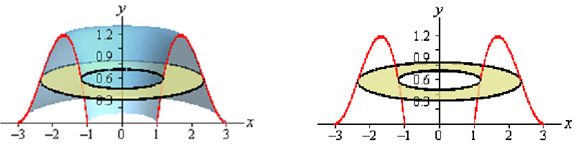
It leads to several problems.  Firstly, both the inner & outer radius is described by the same function. It, in itself, can be dealt along with on occasion.  Although, usually this means more work than other methods so it's frequently not the best approach.

It leads to the second problem we got here. To use rings we would have to put this function into the form x = f ( y ) . Generally that is NOT easy for cubic polynomial and in other cases might not even be possible to do.   Even while it is possible to do this the resulting equation is frequently significantly messier than the original that can also cause problems.

To this point the limits of integration have always been intersection points which were fairly easy to determine.  However, in this case the highest point out is not an intersection point, however instead a relative maximum.  

Therefore, we've seen three problems along with rings in this case which will either increase our work load or outright prevent us from utilizing rings.

What we have to do is to determine a different way to cut the solid which will give us a cross-sectional area that we can work with. One way to do this is to think of our solid as a lump of cookie dough and rather than cutting it perpendicular to the axis of rotation we could instead center cylindrical cookie cutter on the axis of rotation & push this down in the solid. Doing this would specified the following picture,

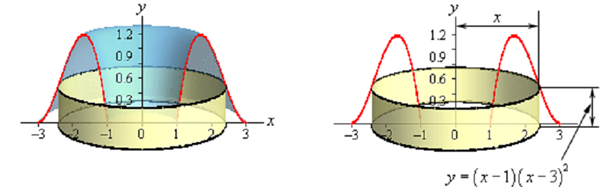
Carrying out this gives us a cylinder or shell in the object and we can simply find its surface area. The surface area of this cylinder is following,

A ( x ) = 2 ∏ ( radius ) ( height )

= 2 ∏ ( x ) (( x -1) ( x - 3)² )

= 2( ( x⁴ - 7 x³ + 15x² - 9 x )

Notice that as we increase the radius of the cylinder we will totally cover the solid and therefore we can use it in our formula to determine the volume of this solid.  All we required are limits of integration. The first cylinder will cut into solid at x = 1 & as we increase x to x = 3 we will entirely cover both sides of the solid as expanding the cylinder in one direction will automatically expand it into the other direction as well.

Then the volume of this solid is,

V = ∫^a_b A(x)dx

= 2 ∏ ∫₁³x⁴  - 7 x³  + 15x²  - 9x dx

= 2 ∏ ( (1/5) x⁵ - (7/4) x⁴ + 5x³ - 9/2 x² |³₁

= 24/5