Find out the volume of the solid obtained by rotating the region bounded by y = x² - 4x + 5 , x = 1 , x = 4 , and the x-axis about the x-axis.

Solution : The firstly thing to do is get a sketch of the bounding region & the solid obtained by rotating the region around the x-axis.  Following are both of these sketches.

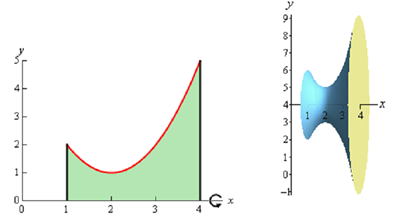
To get a cross section we cut the solid at any x.  Below are some sketches illustrating a typical cross section. The sketch on the right illustrates cut away of the object along with a typical cross section without the caps. The sketch on the left illustrates just the curve we're rotating in addition to its mirror image along the bottom of the solid.

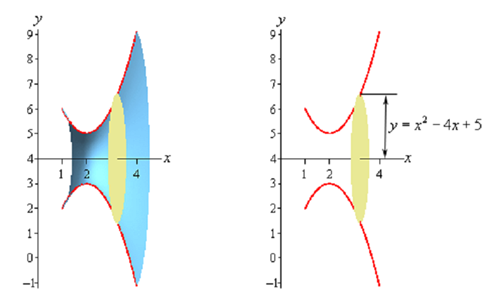
In this case the radius is simply the distance from the x-axis to the curve & it is nothing more than the function value at that particular x as illustrated above.  The cross-sectional area is then,

A ( x ) = ∏ ( x² - 4 x + 5)²  = ∏ ( x⁴ - 8x³ + 26 x² - 40x + 25)

Next we have to determine the limits of integration. Working out from left to right the first cross section will takes place x = 1 and the last cross section will occur at x = 4 .  These are the limits of at integration.

Then the volume of this solid is,

V = ∫_a^b   A ( x ) dx      

= ∏ ∫₁⁴ x⁴  - 8x³  + 26x²  - 40 x + 25 dx

= ∏ ( 1/5 x⁵ - 2 x⁴ + (26/3) x³ - 20 x² + 25x )|⁴₁

= 78 ∏ /5