Find out the reactions at point:

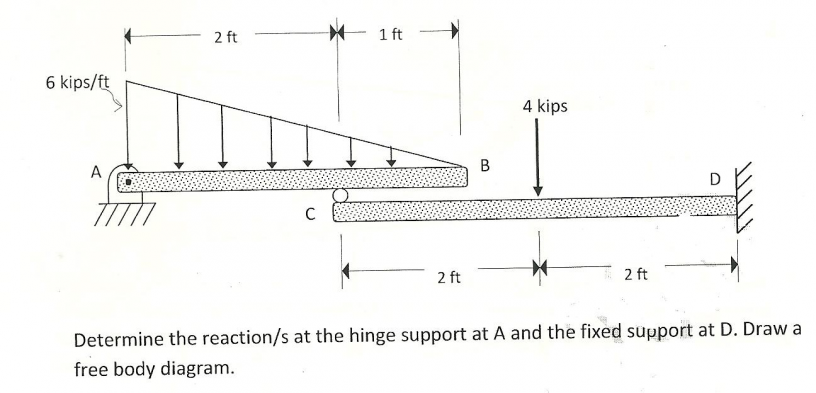
A beam AB is hinged at A and is supported at C. It is loaded as revealed in Figure. Find out the reactions at A and C.

Solution

Let the reaction components at A be H_A and V_A as illustrated in Figure. The reaction at C shall be acting vertically upwards. As the beam is at rest under the action of the forces, the conditions of equilibrium may be applied.

Taking moments of all of forces about A, we obtain

∑ M _A  = 0

18 × 3 × (3/2) + (40 sin 60^o ) × 5 - R_c × 7 + 24 × 9 = 0

∴ 81 + 173.2 - 7 R_c + 216 = 0

∴ R_c = (81 + 173.2 + 216) /7

= 67.171 kN

 [Note : Moments because of H_A, V_A and 40 cos 60^o regarding A are zero as they pass through point A. Clockwise moments are taken as +ve.]

Now, ∑ Fx  = 0

∴ H _A - 40 cos 60^o  = 0

∴ H _A = 40 × 0.5 = 20 kN

and, ∑ F_y  = 0

∴ V_A  - (18 × 3) - 40 sin 60^o  + R_c  - 24 = 0

∴ V_A  = 54 + 34.64 - 67.171 + 24

= 45.469 kN

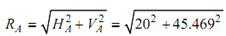
 = 49.673 kN

tan θ= V_A / H _A = 45.469/20  = 2.2734

∴ θ = 66.257^o  = 66^o 15′ 25′′

The reaction at A contain a magnitude of 49.673 kN and is inclined at 66^o 15′ 25′′ with respect to horizontal whereas reaction at C is working vertically upwards and has a magnitude of 67.171 kN.