Example of Probability

Illustration:  It has been determined that the probability density function for the wait in line at a counter is specified by,

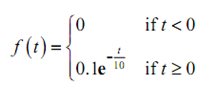
In which t is the number of minutes spent waiting in line. Solve each of the following questions concerning to this probability density function.

(a) Prove that this is in fact a probability density function.

(b) Find out the probability that a person will wait in line for at least 6 minutes.

(c) Find out the mean wait in line.

Solution

(a) Prove that this is in fact a probability density function.  

This function is evidently positive or zero and so there is not much to do here other than calculate the integral.

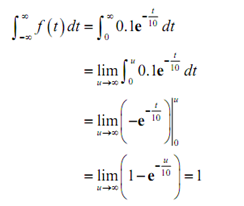
Thus it is a probability density function.  

(b) Find out the probability that a person will wait in line for at least 6 minutes. The probability that we're searching for here is P (x > 6).

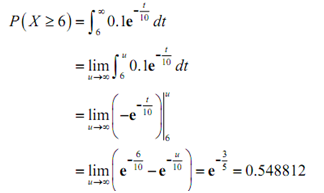
Thus the probability that a person will wait in line for much more than 6 minutes is 54.8811%.

(c) Find out the mean wait in line. 

 Here is the mean wait time.

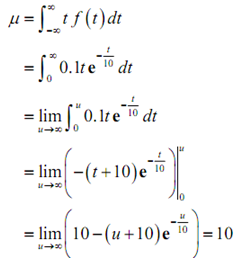
Thus, it looks like the average wait time is 10 minutes.