Find out the maximum deflection in beam:

A beam of span 8m is loaded with UDL of 10 kN/m over the middle half portion. Discover the maximum deflection. EI is constant.

Solution

By symmetry,

R_A  = R_B

= (10 × 4 )/2

= 20 kN

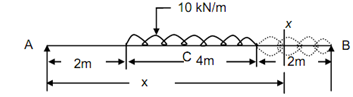
Figure

M = 20 x -(10 ( x - 2)²) /2-(10 ( x - 6)²)/2

= 20 x - 5 ( x - 2)²  - 5 ( x - 6)²                        ---------(1)

EI ( d ² y/ dx²) = M= 20 x - 5 ( x - 2)²  - 5 ( x - 6)²         -------- (2)

EI dy/ dx = 20 x² /2- 5 ( x - 2)³ /3-( 5/3) ( x - 6)³ + C₁         . . . (3)

EIy = 10 x³ /3- (5/12)  ( x - 2)⁴  - (5/12)  ( x - 6)⁴  + C₁  x + C ₂          --------- (4)

at A,  x = 0,     y = 0,        C2  = 0

at B,    x = 8 m,      y = 0

0 =10 × 8³/3 - (5 /12 ) (8 - 2)⁴  - (5/12 )  (8 - 6)⁴  + C₁  × 8

C₁ = - 145

EI (dy/ dx) = 10 x2/3  - (5/3) ( x - 2)3  - (5 /3)( x - 6)3  - 145

EIy = 10 x ³  /3 - (5 /12) ( x - 2)⁴  - (5/12)  ( x - 6)⁴  - 145 x

The maximum deflection at centre, since the beam is symmetrical and symmetrically loaded.

∴          EIy_max  =((10 × 4³ )/3) - (5/12)  (4 - 2)⁴  -  (5/12) ( 4 - 6)⁴  - 145 × 4

y_max= - 1120/3EI