Find out the linear approximation for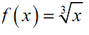 at x =8 .  Utilizes the linear approximation to approximate the value of  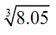and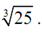

Solution

Since it is just the tangent line there actually isn't a lot to determining the linear approximation.

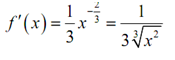                       f (8) = 2                           f ′ (8) = 1/12

The linear approximation is then,

L ( x ) = 2 +(1/12) (x - 8) =(1/12) x + (4/3)

Now, the approximations are nothing more than plugging the specified values of x into the linear approximation. For comparison cause we'll also calculate the exact values.

L (8.05) = 2.00416667 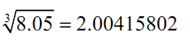          L ( 25)= 3.41666667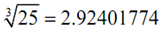              

Therefore, at x = 8.05 this linear approximation does a good job of approximating the actual value. Though, at x= 25 it doesn't do such a good job.

It shouldn't be too astonishing if you think about.  Near x = 8 both the function and the linear

approximation have nearly the similar slope and as they both pass through the point (8, 2) they ought to have nearly the similar value as long as we stay near to x = 8 . Though, as we move away from x = 8 the linear approximation is a line and therefore will always have the similar slope whereas the function's slope will change as x changes and therefore the function will, in all probability, move away from the linear approximation.

Following is a quick sketch of the function & its linear approximation at

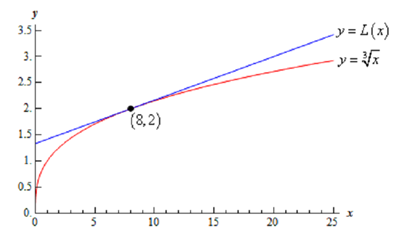
As noted above, the beyond from x = 8 we get the more distance separates the function itself & its linear approximation.