Find out the domain of each of the following.

 (a) f (x,y) = √ (x+y)

(b) f (x,y) = √x+√y

 (c) f (x,y) = ln (9 - x² - 9y²)

Solution

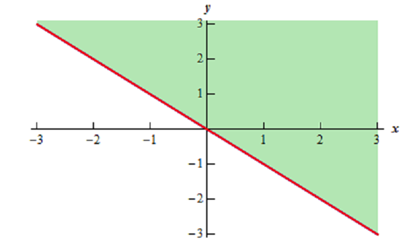
(a) In this example we know that we cannot take the square root of a negative number thus this means that we must need,

x + y > 0

 Here is a diagram of the graph of this region.

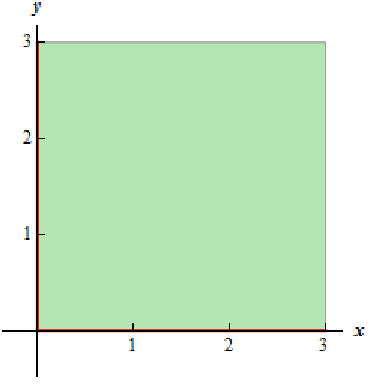
(b) This function is not same from the function in the previous part.  Here we must need that,

 x ≥ 0   and  y ≥ 0

 and they actually do need to be separate inequalities. There is one for every square root in the function. 

Here is the diagarm of this region.

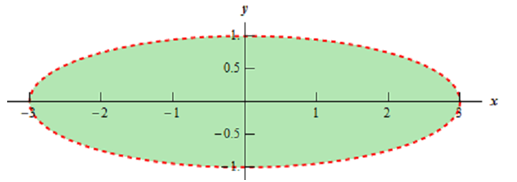
(c) In this last part we are familiar with that we cannot take the logarithm of a negative number or zero (0). Hence we need to require that,

9 - x² - 9y² > 0                  ⇒ x² /9 + y² < 1

and on rearranging we see that we require to stay interior to an ellipse for this function.

Here is a diagram of this region.