We have to enclose a field along with a fence. We contain 500 feet of fencing material & a building is on one side of the field & thus won't require any fencing. Find out the dimensions of the field which will enclose the largest area.
Solution
In the problems we will contain two functions. The first is the function which we are in fact attempting to optimize and the second is the constraint. Sketching out the situation will frequently help us to arrive at these equations thus let's do that.
In this problem we desire to maximize the area of a field & we know that will utilizes 500 ft of fencing material. Therefore, the area will be the function we are attempting to optimize and the amount of fencing is the constraint. The two equations for these are following,
Maximize : A = xy
Contraint : 500 = x + 2 y
We know how to determine the largest or smallest value of any function provided only it's got a single variable. The area function (as well as the constraint) contains two variables in it and so what we know about determining absolute extrema won't work. Though, if we solve out the constraint for one of the two variables we can substitute it into the area and then we will have a function of a single variable.
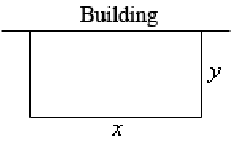
Thus, let's solve out the constraint for x. Note as well that we could have just as easily solved out for y however that would have led to fractions and therefore, in this case, solving for x will possibly be best.
x = 500 - 2 y
Substituting this in the area function specified a function of y.
A ( y ) = (500 - 2 y ) y = 500 y - 2 y 2
Now we desire to find the largest value it will have on the interval [0,250]. Note as well that the interval corresponds to taking y = 0 (i.e. no sides to the fence) and y = 250 (that means only two sides & no width, also if there are two sides each have to be 250 ft to utilizes the whole 500ft).
Note as well that the endpoints of the interval won't make any sense through a physical standpoint if actually we desire to enclose some area since they would both give zero area. However, they do give us a set of limits on y and thus the Extreme Value Theorem tells us that we will contain a maximum value of the area somewhere among the two endpoints.
Thus, recall that the maximum value of a continuous function (that we've got here) on a closed interval (that we also have here) will take place at critical points and/or end points. As already we've pointed out the end points in this case will give zero area and therefore don't make any sense. That means our only alternative will be the critical points.
Thus let's get the derivative and determine the critical points.
A′ ( y ) = 500 - 4 y
Setting this equivalent to zero & solving gives a lone critical point of y = 125. Plugging this into the area specified an area of 31250 ft2. Therefore according to the method this have to be the largest possible area, as the area at either endpoint is zero.
At last, let's not forget to obtain the value of x and then we'll contain the dimensions since this is what the problem statement asked for. We can obtain the x by plugging in our y into the constraint.
x = 500 - 2 (125) = 250
The dimensions of the field which will give the largest area, subject to the fact which we used exactly 500 ft of fencing material, are 250 x 125.