Find out their common velocity:

An aeroplane weighing 40 kN horizontally moves with a velocity of 20 m/sec (72 kmph, that means 72 km per hour). A helicopter of weight 20 kN is proceeding at 30 m/sec (108 kmph) towards North in the same horizontal plane & collides with aeroplane. If the two masses get entangled after collision, find out their common velocity.

Solution

As momentum is a vector along the direction of the velocity of the mass, while the momenta M₁ and M₂ of the aeroplane and the helicopter, respectively, are along two different directions of the two masses, vector rules have to be adopted to determine its resultant momentum.

M¯₁ =(Momentum of aeroplane before collision in units (kg m/sec) along  )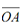

= (40 × 20 )/ g  × 1000

M¯ ₂  =  (Momentum of helicopter before collision along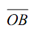in (kg m/sec))

= (20 × 30)/ g  × 1000

The combined mass = (60 × 1000)/ g    kg

Therefore, if M _c is the resultant momentum along direction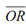 at ∠ α with OA then

V¯c is the common velocity along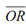

                                                  ∴ M¯ c  = M¯₁ + M¯ ₂

1000 × (60/g) V¯_c = [(40  × 20 )/g +( 20 × 30)/g (OB ↑)]× 1000

This is a vector addition,

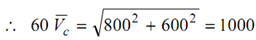
∴ Vc  = 100 /6= 16.67 m / sec along OR

where,

tan α = AR/ OA  = 600 /800 = 0.75

∴          α = 36^o.87