Find out the axial moment of inertia:

Find out the axial moment of inertia of a rectangular area of base b and height d around centroidal axis GX and the base B₁B₂.

Solution

With Reference to Figure, where centroidal axis GX divides the area at mid-depth, i.e. d/2.

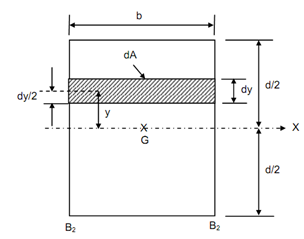
Figure

For a thin strip, illustrated shaded, of width b and thickness (very small) dy, all of the points on it are at a constant distance y from axis GX,

                                                          ∴ dA = bdy

Letting y as positively upward from centroidal axis GX: for elements below

GX, y shall be treated as negative.

                                                        ∴ ∫   A dy = 0

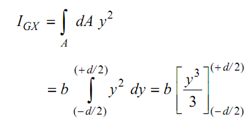
                                                                         =bd³ /12

Likewise, referring to y axis through centroid G,

                                                       I_GY  =   db3 /12

Moment of inertia around base B₁ B₂ may be computed either directly or by utilizing parallel axis theorem.

Direct approach is as. Referring to Figure,

I B₁ B₂   = ∫ dA × ( y′)²

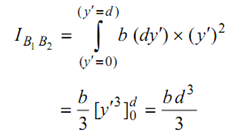
On the other hand, using theorem of parallel axis, we have

I B₁ B₂ = I_GX  + A ( y₁ )²

Where y₁  =  d/2 = perpendicular distance between GX and B₁B₂.

= b d ³/12 + b d (d/2)²           ?

= b d ³/ 3