Find out the area of the region enclosed by y = x2 & y =√x .
Solution
Firstly, just what do we mean by "area enclosed by". This means that the region we're interested in must have one of the two curves on every boundary of the region. Therefore, following is a graph of the two functions along with the enclosed region shaded.
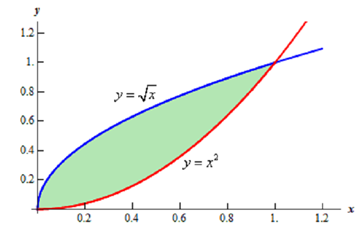
Note as well that we don't take any part of the region to the right of intersection point of these two graphs. In this region there is not any boundary on the right side and therefore is not part of the enclosed area. Remember that one of the specified functions have to be on the each boundary of enclosed region.
Also from this graph it's apparent that the upper function will be based on the range of x's that we utilizes. Due to this you have to always sketch of a graph of the region. Without a sketch it's frequently easy to mistake which of the two functions is the larger. In this case most would possibly say that y = x2 is the upper function and they would be right for the enormous majority of the x's.
Though, in this case this is the lower of the two functions.
The limits of integration for this will be the intersection points of the two curves. In this case it's pretty simple to see that they will intersect at x = 0 & x =1 so these are the limits of integration.
Therefore, the integral that we'll need to calculate to find the area is,
A = ∫ba (Upper function) - (lower function) dx
=∫10 √x-x2 dx
=(2/3x3/2 - 1/3x3)|10
=1/3