Find out Moment of Inertia of circular area:

Find out Moment of Inertia of circular area of radius a = 10 cm about its centroidal axis OX as illustrated in Figure

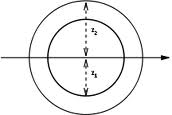
Solution

 Let a thin strip of width B_y at distance y from axis OX where,

y = a sin θ    and      B_y  = 2 (a cos θ)

∴ dy = a cos θ d θ

dA =  B_y  dy = (2 a cos θ) a cos θ d θ

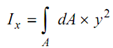
All elements ought to be considered for values of θ ranging from - 90^o to + 90^o + 90^o

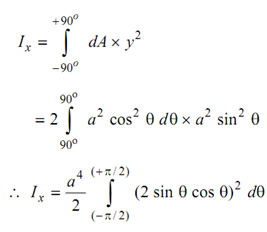
Now that

cos 2 θ = cos² θ - sin ² θ = 2 cos² θ - 1

∴ 2 cos² θ = 1 + cos 2 θ

and,

cos 4 θ = 1 - 2 (sin 2 θ)²

∴ 2 (sin 2 θ)²  = 1 - cos 4 θ

∴ I_x   =  a⁴/2 ∫  2 [ sin 2 θ]²  d θ =  a⁴/2 ∫ (1 - cos 4 θ) d θ

= π a ⁴ / 4

= π D ⁴/64 ,  where D = diameter of circle = 2 a

∴ I _x = π× 10 ⁴ /4 = 7854 cm4 .

This is to be noted down that circular cross-section is axis-symmetric, that means it is symmetric w.r.t. both x and y axes or any other radial direction and also has similar nature of shape regarding all centroidal axes.

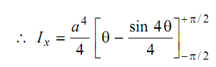
∴ I_y   = I_x   =  πa⁴  /4= π a²   (a²/4) =   A (a²/4)        

where, A = Area of the circle of radius a.

Letting perpendicular axis theorem, we have following :

I _z  = I _x  +  I _y  =  A (a²/2)