Find out its centre of gravity:

A square plate of uniform thickness and density is bent along M₁ M₂ till corner C coincides along with centre C′. Find out its centre of gravity.

Solution

 Consider w be the uniform weight of the plate per unit area. The whole plate after it is

bent can be considered to be made up of three parts.

            (i)         W₁ = Weight corresponding to a square plate OACB

                                = (36 w) at location (3, 3)

             (ii)       W₂ = Weight corresponding to overlapped portion M₁ C ′ M₂

                                 = (4.5 w) at location (4, 4)

             (iii)      (- W₃) = Portion (M₁ C M₂) which is eliminated

                                 = (- 4.5 w) at location (5, 5)

∴          Resultant W = ∑ W_i  = (W₁ + W₂  - W₃ ) = 36 w .

Table

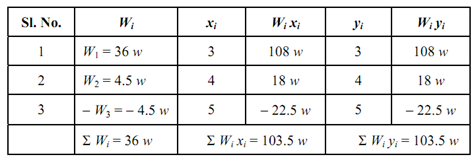
                            ∴ x¯  =103.5/36 =2.88

and, also                  y = 2.88 m .

The example may also be solved with other choice way by considering overall plate as follows:

(i)                  W₁′ = weight of rectangular plate (BM2 M3 O)

                    18 w with its mass-centre at (1.5, 3)

(ii)               W₂′ = weight of square plate (C′′ M₁ AM₃)

                     = 9 w with its mass-centre at (4.5, 1.5)

(iii)             W₃′ = weight of two triangular plates (M₁ M₂ C′′)

                        = 9 w with its mass-centre at (4, 4)

Note that resultant weight W = ∑ w_i  = (18 + 9 + 9) w = 36 w , as before.