Find out where the following function is increasing & decreasing.
A (t ) = 27t 5 - 45t 4 -130t 3 + 150
Solution
As with the first problem first we need to take the derivative of the function.
A′ (t ) = 135t 4 -180t 3 - 390t 2 = 15t 2 (9t 2 -12t - 26)
Next, we have to determine where the function isn't changing. It is at,
t = 0
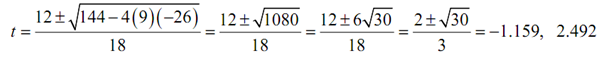
Thus, the function is not changing at three values of t. At last, to find out where the function is increasing or decreasing we have to determine where the derivative is +ve or -ve.
Recall that if the derivative is +ve then the function have to be increasing & if the derivative is -ve then the function have to be decreasing. The given number line gives this information.
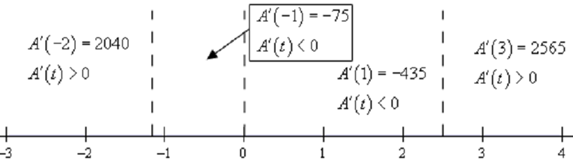
Thus, from this number line we can illustrate which we have the given increasing & decreasing information.
Increasing : - ∞ < t < -1.159, 2.492 < t < ∞
Decreasing : -1.159 < t < 0, 0