Find out Deflection under the load:

A beam of span 4 m is subject to a point load of 20 kN at 1 m from the left support and a Udl of 10 kN/m over a length of 2 m from the right support.

Find out :

1. Slope at the ends.

2. Slope at the centre.

3. Deflection under the load.

4. Deflection at the centre.

5. Maximum deflection.

Take EI = 20 × 10⁶ N-m².

Solution

∑ Fy  = 0, so that R_A + R_B  = 20 + 10 × 2 = 40 kN         --------- (1)

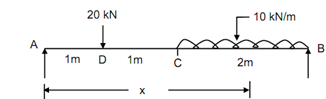
Figure

Taking moments around A,

R_B  × 4 = 20 × 1 + 10 × 2 × 3 = 80

R_B  = 20 kN                                                      -------- (2)

R_A  = 20 kN

M = 20 x - 20 [ x - 1] - 10 [ x - 2] ([ x - 2]/2)

= 20 x - 20 [ x - 1] - 5 [ x - 2]²

EI (d ² y/ dx²) = M

= 20 x - 20 [ x - 1] - 5 [ x - 2]²       ---------- (4)

 EI (dy / dx )= 10 x² /3 - (10/3) [ x - 1]²  - (5/3) [ x - 2]³  + C₁        ------ (5)

EIy = 10 x³ /3- (10/3) [ x - 1]³  - ( 5/12) [ x - 2]⁴  + C ₁ x + C₂  ---------6

at A, x = 0,      y = 0,        C₂  = 0

at B, x = 4 m,      y = 0

0 =(10 × 4³ )/3- 10 (4 - 1)³ - (5/12)  (4 - 2)⁴  + C ₁ × 4

C₁ =- 29.17

EI dy/ dx = 10 x²  - 10 [ x - 1]²  - (5 /3 )[ x - 2]³  - 29.17

 (a)       Slope at A, (x = 0),

θ _A = - 29.17 / EI = - 29.17 × 10/(20 × 10⁶)

 = - 1.46 × 10^{- 3}  radians

(b)        Slope at B, (x = 4 m),

EI θ_B  = 10 × 4²  - 10 (4 - 1)²  - 5 (4 - 2)³  - 29.17 = + 27.5

θ_B = + 1.38 × 10^{- 3}  radians

 (c)       Slope at centre, (x = 2 m),

EI θ_C  = 10 × 2²  - 10 (2 - 1)²  - 29.17

θ_C  = + 0.04 × 10^{- 3}  radians

Deflection under the load :

EIy = 10 x³ /3- 10 [ x - 1]³  - (5/12)  [ x - 2]⁴  - 29.17 x

At x = 1 m,

EIy _D = (10/3) - 29.17

EIy_D  = - 25.84 × 10³ × 10³/20 × 10⁶

= - 1.29 mm

 (d)      Deflection at the centre :

           x = 2 m

EIy =10 × 2³ - (10/3) (2 - 1)³ - 29.17 × 2

y_C  = - 1.75 mm

 (e)       Maximum deflection : Let the maximum deflection b/w D and C (x < 2 m).

dy/ dx = 0

10 x²  - 10 ( x - 1)²  - 29.17 = 0

10 x²  - 10 x²  - 10 + 20 x - 29.17 = 0

x = 1.96 m < 2 m

EIy _max = (10/3) (1.96)³  - 10 (1.96)³  - 29.17 × 1.96 = - 35

∴ y_max  = - 1.7501 mm