Find out all the critical points for the function.
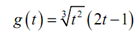
Solution
To determine the derivative it's probably simple to do a little simplification previous to we in fact differentiate. Let's multiply root through the parenthesis & simplify as much as possible. It will let to ignore using the product rule while taking the derivative.
g (t ) = t (2/3) ( 2t -1) = 2t (5/3) - t (2/3)
Now differentiate.
g′ (t ) =(10/3)t(2/3) -(2/3)t(-1/3) = 10t(2/3)/3 -(2/3t(1/3))
We will have to be careful with this problem. While faced along a negative exponent it is frequently best to removes the minus sign in the exponent as we did above. It isn't actually needed but it can make our life simple on occasion if we do that.
Notice that removal the negative exponent in the second term let us to correctly recognize why t = 0 is a critical point for this function. Once we move second term to the denominator we can apparently see that the derivative doesn't exist at t = 0 and so this will be a critical point. If you don't get rid of the -ve exponent in the second term several people will wrongly state that t = 0 is a critical point since the derivative is zero at t = 0 . Whereas it may seem like a silly point, after all in each of case t = 0 is identified as a critical point, it is occasionally important to know why a point is a critical point. Actually, in some sections we'll illustrates a fact that only works for critical points wherein the derivative is zero.
Thus, we've found one critical point (where the derivative doesn't present), however now we have to determine where the derivative is zero (provided it is certainly...). To help with this usually it's best to combine the two terms into a single rational expression. Thus, getting a common denominator & combining gives us,
g′ (t ) =10t-2/3t(1/3)
Notice that still we have t = 0 as a critical point. Doing this kind of combining has to never lose critical points; it's just being done to help us determine them. As we can illustrate now it's become much easier to rapidly determine where the derivative will be zero. Recall as well that a rational expression will just be zero if its numerator is zero
Thus, in this case we can illustrates that the numerator will be zero if t =(1/5) and hence there are two critical points for this function.
t = 0 and t = 1/5