Find out a series solution for the following differential equation about x₀ = 0

y′′ + y = 0.

 Solution

Note that in this case p(x)=1 and therefore every point is an ordinary point. We will be searching for a solution in the form,

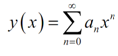
We will require plugging this in our differential equation therefore we'll require to get a couple of derivatives.

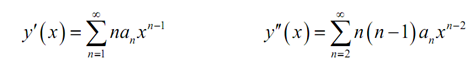
Recall by the power series review section on power series which we can start these at n=0 if we require to, however it's almost all time best to start them where we have now.  If this turns out that this would have been simple to start them at n=0 we can simply fix this up while the time comes around.

Therefore, plug these in our differential equation. Doing it gives,

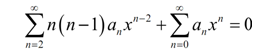
The subsequent step is to combine everything in a particular series. To do that needs which we get both series starting at similar point and that the exponent on the x be similar in both series.

We will all the time start this through getting the exponent on the x to be similar. This is usually best to find the exponent to be an n. The second series previously has the correct exponent and the first series will require to be shifted down through 2 in order to find the exponent up to an n.  If you don't recall how to do it take a rapid look at the first review section where we did some of these kinds of problems.

Shifting the first power series provides us,

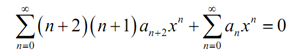
Remember that in the method of the shift we also found both series starting at similar place. It won't always occur, but when it does we'll take this. We can here add up the two series. It gives us subsequent,

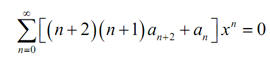
Here recalling the fact from the power series review section we identify that if we contain a power series which is zero for all x as it is, then all the coefficients should have been zero to start with. It gives us the subsequent,

 (n + 2) (n + 1)a_n+2 +a_n =0,                               n = 0,1,2,......

These are termed as the recurrence relation and remember that we contain the values of n for that it should be true. We will all the time want to contain the values of n for that the recurrence relation is true as they won't all the time start at n = 0 as this did in this case.

Here let's recall what we were after in the initial place. We needed to get a series solution to the differential equation. So as to do this we required to find out the values of the a_n's. We are almost to the point where we can do this. The recurrence relation has two dissimilar a='s in this therefore we can't just solve this for a_n and find a formula which will work for all n.  We can though, use this to determine what all but two of the a='s are.

To do that we first solve the recurrence relation for the a_n which has the largest subscript.  Doing it gives as,

a_n+2 = (- (a_n))/((n + 2) (n + 1))                          n = 0,1,2,......

Currently, at this point we just require to start plugging in several values of n and notice what occurs,

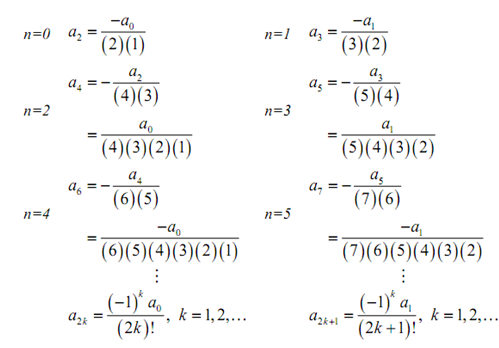
See that at each step we all the time plugged back into the earlier answer hence when the subscript was even we could all the time write thea_n in terms of a₀ and while the coefficient was odd we could all the time write the a_n in terms of a₁. Also see that, during this case, we were capable to get a general formula for a_n's with even coefficients and a_n's with odd coefficients. It won't always be probable to do.

Now here is one more thing to notice. The formulas which we developed were simply for k=1,2,... though, in this case again, they will as well work for k=0. Again, it is something that won't forever work, but does now.

Do not get excited regarding to the fact which we don't know what a₀ and a₁ are.  As you will notice, we actually require these to be in the problem to find the accurate solution.

Here that we've found formulas for the a_n's let's find a solution. The first thing which we'll do is write out the solution along with a couple of the a_n's plugged into.

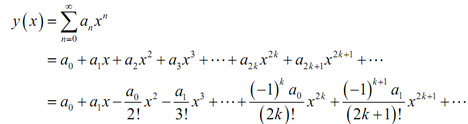
The subsequent step is to collect all the terms along with similar coefficient in them and then factor out that coefficient.

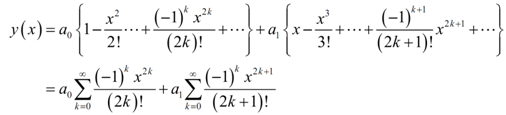
In the previous step we also used the fact which we knew what the common formula was to write both portions like a power series.