Extreme Value Theorem : Assume that f ( x ) is continuous on the interval [a,b] then there are two numbers a ≤ c, d ≤ b so that f (c ) is an absolute maximum for the function and f ( d ) is an absolute minimum for the function.

Thus, if we contain continuous function on an interval [a,b] then we are guaranteed to contain both an absolute maximum & an absolute minimum for the function somewhere within the interval. The theorem doesn't described where they will takes place or if they will take place more than once, however at least it tells us that they do present somewhere.  Sometimes, all that we need to know is that they do present.

This theorem doesn't say anything regarding absolute extrema if we aren't working on an interval. We saw instance of functions above that had both absolute extrema, one absolute extrema, & no absolute extrema while we didn't limit ourselves down to an interval.

The requirement which a function be continuous is also needed in order for us to use the theorem. Consider the case of

                                            f ( x ) =  1 /x²              on    [-1,1]

Following is the graph.

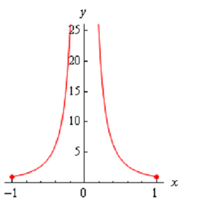
At x = 0 this function is not continuous as we move in towards zero the function is approaching infinity.  Thus, the function does not contain an absolute maximum.  Note as well that it does have an absolute minimum though.  Actually the absolute minimum takes places twice at both x = -1 & x = 1 .

If we changed the interval just a little to say,

f ( x ) =  1 /x² on          [ 1/2 , 1]

now the function would have both absolute extrema. We might only run into problems if the interval has the point of discontinuity.  If this doesn't then the theorem will hold.

We have to also point out that just because the reason a function is not continuous at a point which doesn't mean that it won't contain both absolute extrema in an interval which contains that point.  Below is the graph of function which is not continuous at a point in the given interval & still has both absolute extrema.

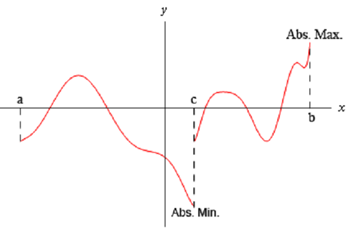
This graph is not continuous at x = c , Still it does have both an absolute maximum ( x = b ) and an absolute minimum ( x = c ).  Also note as well that, in this case one of the absolute extrema taken places at the point of discontinuity, however it doesn't required to. The absolute minimum could only have easily been at the other ending point or at some other point interior to the region. The point is here that this graph is not continuous and until now does have both absolute extrema

The point of all this is that we required to be careful to just use the Extreme Value Theorem while the conditions of the theorem are satisfied & not misinterpret the results if the conditions aren't satisfied.

In order to utilize the Extreme Value Theorem we ought to have an interval & the function have to be continuous on that interval. If we don't contain an interval and/or the function isn't continuous on the interval then the function may or may not contain absolute extrema.