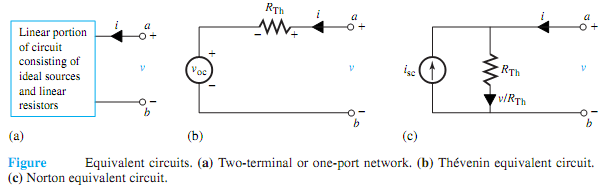
Q. Explain Thevenin and norton equivalent circuits?

For a linear portion of a circuit consisting of ideal sources and linear resistors, the volt-ampere (v-i) relationship at any two accessible terminals can be expressed by the linear equation

v = Ai + B

where A and B are two constants. The Thévenin equivalent circuit at any two terminals a and b (to replace the linear portion of the circuit) is given by

v = R_Thi + v_oc

where it can be seen that

R_Th = v/i|_voc = 0

and

voc = v|_i=0

Thus, voc is known as the open-circuit voltage (or Thévenin voltage) with i = 0, and R_Th is the Thévenin equivalent resistance (as seen from the terminals a-b) with voc = 0. Equation accounts for the ideal sources present in that linear portion of the circuit, as shown in Figure (a), where as Equation implies deactivating or zeroing all ideal sources (i.e., replacing voltage sources by short circuits and current sources by open circuits). Themodel with the voltage source voc in series with RTh is known as Thévenin equivalent circuit, as shown in Figure(b).

Equation may be rewritten as

i = v / A - B / A = v / R_Th - v_oc / R_Th = v / R_Th - isc

which is represented by the Norton equivalent circuit with a current source isc in parallel with RTh, as shown in Figure. Notice that with v = 0, i = -i_sc. Also, i_sc = v_oc/R_Th,or v_oc = i_scR_Th.