With the help of R-2R binary network, explain the working of a 3-bit D/A converter and derive an expression for the output voltage.

Ans:

We see a 3-bit R-2R ladder D/A network shown in Fig.(a).In this circuit we have assumed that the digital input as 001.

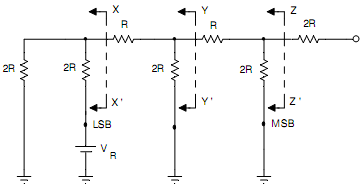
Fig.(a) 3 bit R-2R Ladder D/A Network

The circuit is simplified by using Thevenin's theorem. By applying Thevenin's theorem on XX', we get the circuit of Fig. (b). Likewise, by applying Thevenin's theorem at YY' and ZZ', we acquire the circuits of Fig.(c) and (d) respectively. Now there, LSB is assumed as 1 and the equal voltage acquired is V_R/2³.

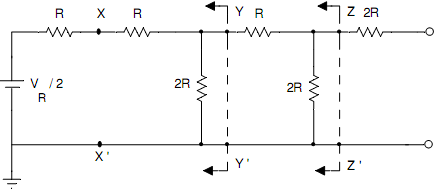
Fig.(b) Equivalent circuit after by applying Thevenin's Theorem at XX'

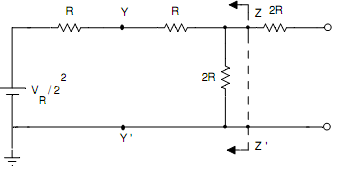
Fig.(c) Equivalent circuit after by applying Thevenin's Theorem at YY'

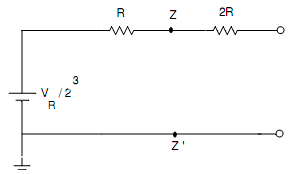
Fig.(d) Equivalent circuit after by applying Thevenin's Theorem at ZZ'

Likewise for the digital input of 010 and 100 the equivalent voltages are V_R/2² and V_R/2¹ correspondingly. The value of the equal resistance is 3R in all cases. Thus, we get an equivalent circuit of 3-bit R-2R Ladder D/A Converter that is specified in Fig.(e). The output analog voltage V_O is given by

V_o = -((R_f/3r).( V_R/2³).b_o +(R_f/3r).( V_R/2²).b₁ +(R_f/3r).( V_R/2¹).b₂ )

V_o = -((R_f/3r).( V_R/2³))[4b₂ + 2b₁ + 1b₀]

Thus the above equation explains that the analog output voltage is proportional to the digital input.

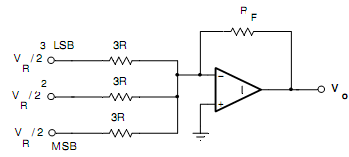
Fig.(e) Equivalent circuit of 3-bit R-2R Ladder D/A Converter