Explain the Phase Diagrams - Ternary Systems?

A ternary system is one with three components. We can independently vary the temperature, the pressure, and two independent composition variables for the system as a whole. A two- dimensional phase diagram for a ternary system is usually drawn for conditions of constant T and p. Although we could draw a two-dimensional phase diagram with Cartesian coordinates to express the mole fractions of two of the components, there are advantages in using instead the triangular coordinates shown in Fig. Each vertex of the equilateral triangle represents one of the pure components A, B, or C. A point on the side of the triangle opposite a vertex represents a binary system of the other two components, and a point within the triangle represents a ternary system with all three components. To determine the mole fraction z_A of component A in the system as a whole represented by a point within the triangle, we measure the distance to the point from the side of the triangle that is opposite the vertex for pure A, then express this distance as a fraction of the height of the triangle. We follow the same procedure to determine z_B and z_C. The concept is shown in Figure. As an aid for the conversion between the position of a point and the overall composition, we can draw equally-spaced lines within the triangle parallel to the sides as shown in Figure. One of these lines, being at a constant distance from one side of the triangle, represents a constant mole fraction of one component. In the figure, the lines divide the distance from each side to the opposite vertex into ten equal parts; thus, adjacent parallel lines represent a difference of 0:1 in the mole fraction of a component, starting with 0 at the side of the triangle and ending with 1 at the vertex. Using the lines, we see that the filled circle in the figure represents the overall composition z_A = 0.20, z_B = 0.30, and

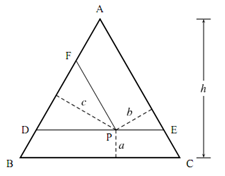
Figure Proof that the sum of the lengths a, b, and c is equal to the height h of the large equilateral triangle ABC. ADE and FDP are two smaller equilateral triangles. The height of triangle ADE is equal to h a. The height of triangle FDP is equal to the height of triangle ADE minus length b, and is also equal to length c: h a b D c. Therefore, a + b + c = h.

z_C = 0.50. The sum of z_A, z_B, and z_C must be 1. The method of representing composition with a point in an equilateral triangle works because the sum of the lines drawn from the point to the three sides, perpendicular to the sides, equals the height of the triangle. The proof is shown in Fig. Two useful properties of this way of representing a ternary composition are as follows:

1. Points on a line parallel to a side of the triangle represent systems in which one of the mole fractions remains constant.

2. Points on a line passing through a vertex represent systems in which the ratio of two of the mole fractions remains constant.