Explain the Electric Forces and Fields
This can be thought of in terms of an electric field, E, similar to the gravitational field discussed earlier [Fg = m g( r ) where at the surface of the Earth g is a vector downward toward the center of the Earth].
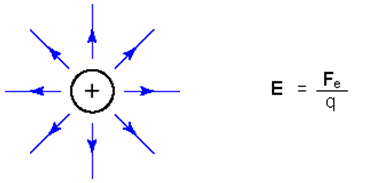
where Fe is the electric force vector in Newtons, q is the charge in coulombs, and E is the electric field vector due to all other charges in Newtons/coulomb. For one charge, Q, Coulomb's Law gives an electric field of
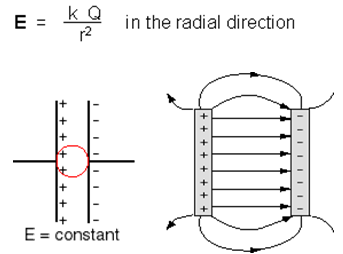
One example when this construct of an electric field becomes very useful is if we have two parallel plates facing one another, one of them charged positively and the other charged negatively. In general, the electric field of many charges together is the sum of the fields of the individual charges. In the parallel plate capacitor's geometry, the electric field can be considered a constant value near the center of the plates away from the edges.
Work in an Electric Field
Work can be done in an electric field just like work is done in a gravitational field. Work is the product of the force and the distance through which the force is applied. In a uniform electric field, like that created between two charged plates, we can use the idea of potential, V, to help us compute the work done. In a parallel plate capacitor, whose plates are a distance, d, apart, the electric field is given by
E = V/d
and the work done in moving a positive charge from the negative plate to the positively charged plate is
W = q V
where W is work in joules, q is the charge in coulombs, and V is the electric potential in volts.