Q. Explain Steady-State Error of Linear Systems?

If the steady-state response of the output does not agree exactly with the steady state of the input, the system is said to have a steady-state error. Steady-state errors in practical control systems are almost unavoidable because of friction, other imperfections, and the nature of the system. The objective is then to keep the error to a minimum, or below a certain value. The steady-state error is a measure of system accuracy when a specific type of input is applied to a control system.

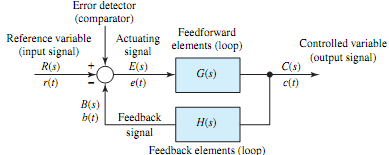
Referring to Figure, assuming the input and output signals are of the same dimension and are at the same level before subtraction, with a nonunity element H(s) incorporated in the feedback path, the error of the feedback control system is defined as

e(t) = r(t) - b(t) or E(s) = R(s) - B(s) = R(s) - H(s)C(s) or using Equation,

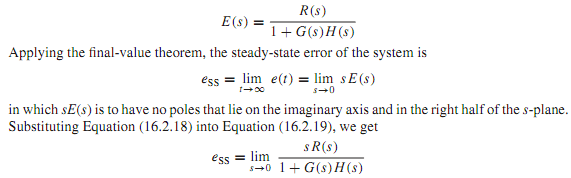
which apparently depends on the reference input R(s) and the loop gain (loop transfer function) G(s)H(s).

The type of feedback control system is decided by the order of the pole of G(s)H(s)at s = 0. Thus, if the loop gain is expressed as

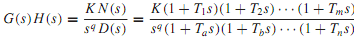
where K and all of the T are constants, the exponent of s, i.e., q, in the denominator represents the number of integrations in the open loop, and the exponent q defines the system type. With q = 0, 1, or 2, the system is classified as position, velocity, or acceleration system, respectively.