Explain Simple Harmonic Motion
Many repeating motion problems can be solved by taking the displacement as
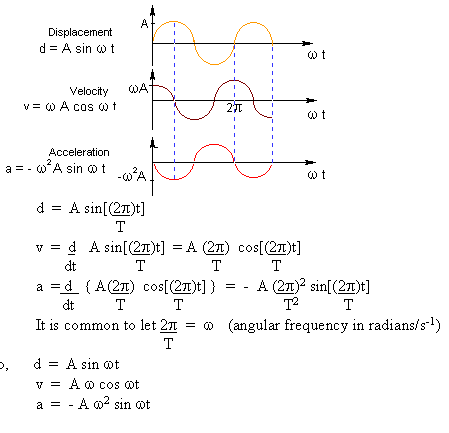
where d is distance in meters, A is amplitude in meters, v is speed in meters per second, a is acceleration in meters per second squared, is the angular frequency in radians/second or just 1/second (Radians may or may not be explicitly stated in the units.) and t is time in seconds. This form of displacement, velocity, and acceleration will work for circular motion, pendulum motion, and spring motion. All these are considered types of simple harmonic motion, where the displacement is directly proportional to the force in the problem. More force gives more displacement, and less force gives less displacement. For springs, this is called Hooke's Law
F = -k Δx
where k is the spring constant (N/m), Δx (in meters) is the change in length of the spring (we use x since this only happens in one dimension), and F (in Newtons) is the force that opposes you (This gives the - sign in the law so that the force is in the opposite direction from the change in length.) when you're trying to stretch or compress the spring.
ω = (K) ½ / m Relates ω and k and m of spring system
where k is the spring constant in N/m, m is the mass of the spring system in kilograms and ω is the angular frequency in inverse seconds.