Potential of Parallelism

Problems in the actual world differ in respect of the amount of inherent parallelism intrinsic in respective problem domain. Some problems can be easily parallelized. Conversely, there are some inherent chronological problems (e.g. computation of Fibonacci sequence) whose parallelization is almost impossible. The extent of parallelism can be enhanced by suitable design of an algorithm to solve the problem consideration. If processes do not share address space and we could get rid of data dependency among instructions, we can attain higher level of parallelism. The idea of speed up is used as a measure of the speed up which indicates up to what extent to which a sequential program can be parallelized.  Speed up can be taken as a sort of amount of inherent parallelism in a program. In that respect, Amdahl has given a law, called Amdahl's Law, according to this law potential program speedup is stated by the fraction of code (P) which can be parallelised:

Speed up= 1 / 1-p

If no part of the code can be parallelized, P = 0 and speedup = 1 it implies that it is an inherently chronological program. If all the code is parallelized then P = 1, the speedup is infinite. However practically, the code in no program is able to make 100% parallel. Therefore speed up cannot be infinite ever.

If 50% of code can be parallelized, maximum speedup = 2, meaning the code would run twice as fast.  

If we set up the number of processors executing the parallel fraction of work, the relationship can be modeled by:

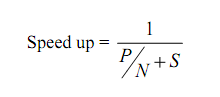
Where P = parallel fraction, N = total number of processors and S = Serial fraction.The Table 1 shows the values of speed up for various values N and P.

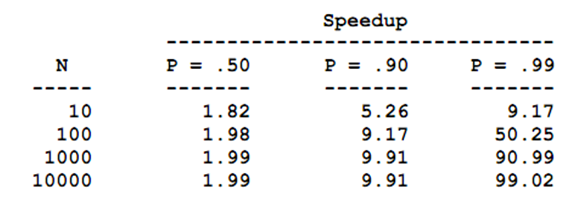
The Table 1 proposes that speed up increases as P increases. Though, after a certain limits N doesn't have much impact on the value of speed up. The reason being that is for N processors to remain active, the code must be in some way or other, be divisible in more or less N parts, independent part, every part taking almost equal amount of time.