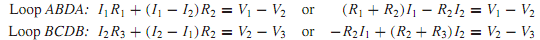Q. Explain Mesh - Current Method?
This complements the nodal-voltage method of circuit analysis. A set of independent mesh-current variables that implicitly satisfy the KCL equations is selected in order to formulate circuit equations in this mesh analysis. An elementary loop,ora mesh, is easily identified as one of the "window panes" of the whole circuit. However, it must be noted that not all circuits can be laid out to contain only meshes as in the case of planar networks. Those which cannot are called nonplanar circuits, for which the mesh analysis cannot be applied, but the nodal analysis can be employed.
A mesh current is a fictitious current, which is defined as the one circulating around a mesh of the circuit in a certain direction. While the direction is quite arbitrary, a clockwise direction is traditionally chosen. Branch currents can be found in terms of mesh currents, whose solution is obtained from the independent simultaneous equations. The number of necessary equations in the mesh-analysis method is equal to the number of independent loops or meshes.
All current sourceswith shunt conductanceswill be replaced by their corresponding Thévenin equivalents consisting of voltage sources with series resistances. Let us illustrate the method by considering a simple, but typical, example, as shown in Figure (a).
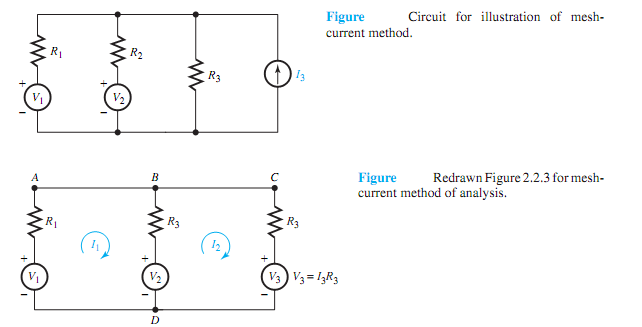
Replacing the current sourcewith shunt resistance by the Thévenin equivalent, Figure (a) is redrawn as Figure (b), in which one can identify two elementary loops, or independent meshes.
By assigning loop or mesh-current variables I1 and I2, as shown in Figure (b) , both in the clockwise direction, one can write the KVL equations for the two closed paths (loops) ABDA and BCDB,