Explain Medium length lines?

Medium length lines cover lines in the range of 50 to 150 miles (80 to 240 km). Due to the increased length of the line, the shunt capacitance of the line is significant and is included in the equivalent circuit model. Therefore, the line model may be represented by a π network, as shown in Figure.

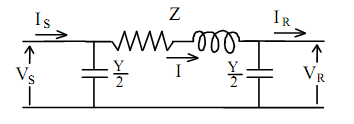
Using Kirchhoff's voltage and current laws, the π circuit gives:

V_S = V_R + Z I         (1)

I = I_R + Y/2 V_R      (2)

I_S = I + Y/2 V_S      (3)

To obtain VS and IS in terms of VR and IR , substitute equation (2) into (1) which gives:

V_S = [(1 + ZY) / 2] V_R + Z I_R                                                    (4)

Substituting equations (4) and (2) into equation (3) and rearranging yields:

I_S = [(1 + ZY) / 4] Y V_R + [(1 + ZY) / 2] I_R        (5)

Comparing equations (4) and (5) with equations gives the 2-port network constants as:

A = [(1 + ZY) / 2], B = Z

C = [(1 + ZY) / 4], D = [(1 + ZY) / 2] = A

Another way of representing a medium length line is by the Τ network shown in Figure. In this case:

V_S = V_C + Z/2 I_S                                              (6)

V_C = V_R + Z/2 I_R   and                          (7)

I_S = I_R + Y V_C                                                   (8)

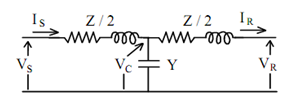
As for the π network, equations (6-8) may be solved and rearranged to obtain V_S and I_S in terms of V_R and I_R as:

V_S = [(1 + ZY) / 2] V_R + [(1 + ZY) / 4] I_R                                           (9)

IS = Y V_R + [(1 + ZY) / 2] I_R                                                                     (10)

This gives the 2-port network constants as:

A = [(1 + ZY) / 2], B = [(1 + ZY) / 4] Z

C = Y, D = [(1 + ZY) / 2] = A