Explain Identifying Conic Sections

The graph of a quadratic equation in the variables x and y, like this one,
x² + 3y² + 6y = -4, is a conic sections. There are three kinds of conic section:
• hyperbola (a pair of bent lines)
• parabola ( a single bent line)
• ellipse ( a bent circle).

You can identify these three types just by looking at the equation.
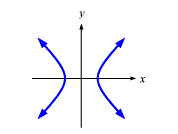
Hyperbolas have equations with both an x2 and a y2 term, and there terms have opposite signs (when written on the same side of the equation). Here are three examples:
x² - y² = 1
-2x² + x + y² = 0
x² + y =2 + y²
And this is what the graph of a typical hyperbola looks like:

Note that if the squared terms in the third example were moved to the same side of the equation, they would have opposite signs.

Ellipses also have equations with both an x2 and a y2 term, and these terms have the same sign. Here are three examples of ellipses:
x² + y² = 1
-2x² + x - y² = 0
x² + y = 2 - y²
Here is the graph of the first example:

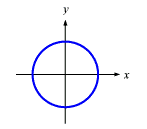
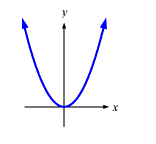
As you can see, some ellipses- the ones that aren't unevenly scaled- are just circles! Parabolas have equations with only one variable (x or y) squared, but not both.
y = x²
-2x - y² = 0
x² + y = 2- y
Graphs of parabolas look something like this:

Note: If the equation has an "xy" term, then you have a rotated conic section. Most calculus courses avoid this somewhat complicated issue, and deal only with non-rotated conics.