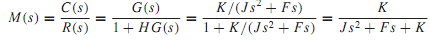Error-Rate Control, Output-Rate Control, and Integral-Error (Reset) Control
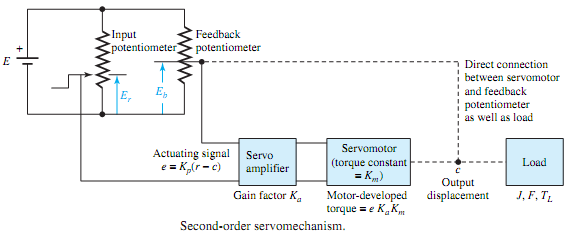
Let us consider a typical second-order servomechanism(containing two energy-storing elements) whose defining differential equation for obtaining the dynamic behavior of the system is given by
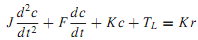
where J, F, and TL represent, respectively, effective inertia, equivalent viscous friction, and resultant load torque appearing at the motor shaft; K = KpKaKm, where Kp is the potentiometer transducer constant (V/rad), Ka is the amplifier gain factor (V/V), and Km is the motor-developed torque constant (N·m/V) of the physical servomechanism shown in Figure; r is the input command and c is the output displacement, both in radians.
The block diagram of the servomechanism of Figure is given in Figure, in which the transfer function of each component is shown. Since the actuating signal is given by E = Kp(R - C), the block diagram may be simplified, as shown in Figure, in which TL is assumed to be zero for simplicity. The direct transmission function (forward path transfer function) for the system can be seen to be
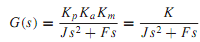
The corresponding closed-loop transfer function is given by