Explain Basic Geometric Concepts ?
Points, lines, and planes are the most fundamental concepts in the study of geometry.
Points

A point has no length, width or height; it indicates a position. A point is usually labeled by a capital letter and represented by a dot. We call the points below point A, point B and point C.
Line

A line is straight and extends infinitely in two opposite directions. A line consists of an infinite number of points; it has no width and no height. The line below is called line a.
Planes
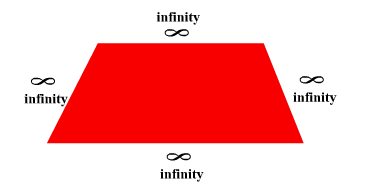
A plane is a flat (2-dimesional) surface, extending infinitely in all directions. A plane consists of an infinite number of points; it has infinite length and width, but no height. Think of a very large sheet of paper.
Spaces

A space is 3 dimensional. It has no boundaries; that is, it has an infinite number of points, and infinite length, width, and height. Think of a very big swimming pool.
Parallel lines

Parallel lines are lines that never intersect. They are always the same distance apart. Think of never ending railroad tracks.
Intersecting lines

Intersecting lines are lines that share at least one point. Think of intersecting roads.
Segments
A segment is made up of two points and all the points between them. It is the same as a line with endpoints.
Rays
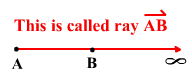
A ray is a part of a line. It begins at a point, called an endpoint, and then extends infinitely in one direction. Think of the ray of light from your flashlight.