My nephew had been introduced to division by his teacher Ms. Santosh, in Class 3. He, and several of his friends who had been taught by her, appeared to be quite comfortable with the concept and process of division when I discussed it with them. This discussion was held about the time my nephew joined Class 5. Since the teacher's method seemed to be effective, I decided to find out the details from her.
When I contacted Ms. Saltosh about this, she was more than willing to share her teaching strategy with us. According to her, it is important to introduce children to division through simple concrete activities. For instance, she asks them to put 30 seeds / leaves / pebbles in groups of 3, and count the number of groups. Then asks them, "How many 3's in 301"
Another activity that she does with them is to divide them into groups of 5, and give each group 20 things (some can be given marbles, others pebbles, etc.). Then she asks one person in the group to divide the objects among all the children in the group. The child counts out 5 marbles, and gives one each to the children. Santosh then asks questions like 'How many sets of five can she take?' and 'How many marbles does each child get?'.
Since the division process is not very well understood, Santosh feels that it is necessary to do many activities of the kind suggested above with children. This should be done in many different contexts, with different objects.
While doing the activities, she keeps conversing with the children and using terms like share, divide by, divide into, how many times, how many are there in, how many groups, split up into equal parts, between, among, etc. She also gives the children several stories involving each of these terms. At a later stage, she encourages the children to create stories involving division.
Once Santosh feels that a child is able to divide up sets of objects, she begins the process of helping her acquire the meaning of the operation. For this, she tries to help the child recognise division as the reverse process of multiplication through activities like the following:
She asks her to divide up a set of 10 matchsticks into sets of 2 each, and asks her how many there are. Next, she asks her to take the 5 sets of 2 matchsticks each and tell her how many in all. She does this kind of activity with LO stones, 10 twigs, ..., till the child begins to see the relationship between '10 divided by 2 is 5' and '2 times 5 is 10'.
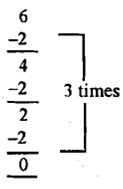
Gradually, through such activities, and with practice, when children are asked to find '6 divided by 2', they try and answer 'how many times does 2 go into 6?'. To answer this, they recite the table of 2 till they get to 6, and therefore, '6 divided by 2 is 3'. Some of them initially answer this by resorting to 'repeated subtraction', that is, for them '6 divided by 2' has the meaning 'how many times can 2 be repeatedly subtracted from 6?', that is, '
Once children have understood what division means in the context of simple situations, Santosh introduces them to the symbol +. Then, to familiarise them with the symbol, and with the relationship between 'x' and 'i', she gives them various activities. For instance, she divides them up into small groups and gives each group a set of cards like asking them to write out a division fact.
She then exchanges a for m and asks them if they can shuffle the cards around to make another statement. (Several versions of this activity are possible.)
She also gives children worksheets to make them practise division / multiplication facts. By assessing the children over a period of time, Santosh finds that this way of learning division ultimately leads them to interpret, say 24 9 3 = 8, in the following ways:
1. If a collection of 24 objects is equally shared among 3 groups, each group will have 8 objects in it.
2. If a collection of 24 objects is divided up into groups of 3 objects each, the result is 8 groups.
3. From 24, 3 can be repeatedly subtracted 8 times.
4. 8 threes are 24.
5. 3 eights are 24.
6. 3 goes 8 times into 24.
One important part that Santosh made, while talking to me, was that the way she exposes children to division does not require them to know multiplication thoroughly before starting division. Some familiarity with multiplication is enough for them to initially see the relationship between the two operations. And, the children continue learning both operations side by side.