Q. Example on hamming error correcting code?

For illustration a 4-bit matching word can stand for 2⁴=16 values that range from 0 to 15 as:

0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111

1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111

Value 0000 or 0 represent no error while other values that are 2ⁱ-1 (for 4 bits 2⁴- 1=15 which is from 1 to 15) signify an error condition. Every one of these 2ⁱ - 1(or 15 for 4 bits) values can be used to signify an error of an individual bit. Because error can take place at the time of transmission of 'N' bit data and 'i' bit error correction code hence we need to have as a minimum 'N+i' error values to signify them. Thus number of error correction bits must be found from subsequent equation:

2ⁱ - 1     >= N+i

If we are presuming 8-bit word then we need to have

2ⁱ - 1     >= 8+i

Say at

i=3                     LHS = 2³ -1 = 7; RHS = 8+3 = 11 

           i=4                      2ⁱ-1 = 2⁴ - 1 = 15; RHS = 8+4 = 12  

Thus for an eight-bit word we need to have as a minimum four-bit error correction code for detecting and correcting errors in a single bit at the time of transmission.

In the same way for 16 bit word we require i = 5

2⁵ -1 = 31 and 16+i = 16+5 = 21

For 16-bit word we require five error correcting bits.

Let's explain this with help of an illustration:

Let's presume 4 bit data as 1010

The logic is displayed in subsequent table:

Source:

This complete information that is (data and P1

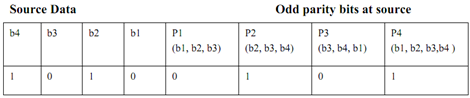
to P4) is transmitted.  

Presuming one bit error in data.

So  P1  - D1, P3 - D3, P4  -D4 pair are different so, as per Figure b1 is in error, so correct it by completing b1 to get correct data 1010.

Case 2:   Data Received as 1000  (Error in b2)

So   P1 - D1, P2 - D2,   P4 - D4 pair are different so as per figure bit b2 is in error.  So correct it by complementing it to get correct data 1010.

Case 3:  

Now let's take a case when data received is correct however on receipt one of parity bit let's say P4 become 0.  Please note in this matter because data is 1010 destination parity bits would be D1=0, D2=1, D3=0, D4=1.  So P1- D1, P2 - D2, P3 - D3 would be same however P4 -D4 are different. This doesn't belong to any of combinations in Figure above. So we conclude P4 received is wrong.