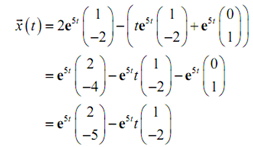Illustration: Solve the following IVP.

Solution:

First get the eigenvalues for the system.

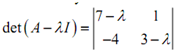
= l² - 10 l+ 25

= (l- 5)²

l_1,2 = 5

Therefore, we got a double eigenvalue. Obviously that must not be too surprising given the section which we're in. here we find the eigenvector for that eigenvalue.

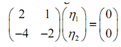
2h₁ +   h₂ = 0,                         ⇒         h₂ = - 2h₁

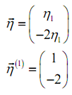
The eigenvector is,

h₁≠ 0

h₁= 1

The next step is get ?r.  To do this we'll require solving,

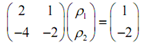
2  ?r₁+  ?r₂ = 1,                       ?r₂ = 1 - 2  ?r₁

Remember that this is almost the same to the system which we solve to find the eigenvalue.  The simple difference is the right hand side. The most common possible ?r is,

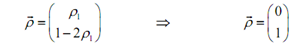
If r₁ = 0

During this case, unlike the eigenvector system we can select the constant to be anything we need, therefore we might as well pick it to create our life easier. This generally means picking this to be zero.

 We can now write down the general solution to the system.

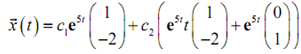
Applying the initial condition to get the constants provides us,

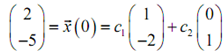
c₁ = 2;

-2 c₁ + c₂ = -5;

By solving both equations we get:

c₁ = 2;

c₂ = -1

The actual solution is,