Any 15 foot ladder is resting against the wall. The bottom is at first 10 feet away from the wall & is being pushed in the direction of the wall at a rate of 1 ft/sec. How rapid is the top of the ladder moving up the wall 12 seconds after we begin pushing?
Solution
The initial thing to do in this case is to sketch picture which demonstrated us what is going on.
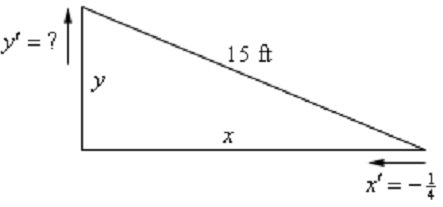
We've described the distance of the bottom of latter through the wall to be x & the distance of the top of the ladder through the floor to be y. Note that these are modifying with time and thus we really have to write x (t ) & y (t ) . However, as is frequently the case with related rates/implicit differentiation problems we don't write down the (t ) part just attempt to remember it in our heads since we proceed with the problem.
Next we must identify what we know and what we desire to find. We know that the rate on which the bottom of the ladder is moving in the direction of the wall. It is,
x′ = - 1/4
Note that the rate is negative as the distance from the wall, x, is decreasing. Always we need to be careful with signs with these problems.
We desire to determine the rate at which the top of the ladder is moving away through the floor. it is y′ . Note that this quantity have to be positive as y will be increasing.
Using Pythagorean theorem.
x2 + y 2 = (15)2 = 225
All that we have to do at this point is to differentiate both of the sides w.r.t. t, remembering that x & y are really functions of t and thus we'll have to do implicit differentiation. Doing this gives an equation that illustrates the relationship among the derivatives.
2xx′ + 2 yy′ = 0 .............(1)
Next, let's see which of the several parts of this equation which we know and what we have to determine. We know x′ & are being asked to determine y′ thus its okay that we don't know that.
Though, still we need to determine x and y.
Finding out x and y is in fact fairly simple. We know that at first x = 10 and the end is being pushed in direction of the wall at a rate of 1/4 ft/sec and which we are interested in what has happened after 12 seconds. We know,
distance = rate ×time
= (1 /4) (12) = 3
Thus, the end of the ladder has been pushed into 3 feet and thus after 12 seconds we have to have x = 7 . Note as well that we could have calculated this in one step as follows,
x = 10 - 1/4 (12) =7
To determine y (after 12 seconds) all that we have to do is reuse the Pythagorean Theorem along with the values of x which we just found above.
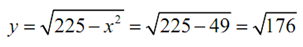
Now all that we ought to do is plug into (1) and solve out for y′ .
2 (7 ) ( -1/4)+2(√176)y' = 0 ⇒ y′ = 7/4/√176 = 7/4√176 = 0.1319 ft/sec
Notice as well that we got the accurate sign for y′. If we'd gotten a -ve then we'd have known that we had committed a mistake and we could go back & look for it.