Example of Partial Fraction Decomposition
Evaluate the following integral.
∫ (3x+11 / x2-x-6) (dx)
Solution:
The 1st step is to factor the denominator so far as possible and acquire the form of the partial fraction decomposition. By doing this gives,
3x + 11 = (x - 3) (x + 2)
A / x - 3 + B/ x + 2
The other next step is to actually add the right side back up.
3x + 11 / (x - 3) (x + 2)
A (x + 2) + B (x - 3) / (x - 3) (x + 2)
Here now, we require to choose A and B that is why the numerators of these two are equal for every x. To do this we'll require to set the numerators equal.
3x + 11 = A (x + 2) + B (x - 3)
Note: In several problems we will go straight from the common form of the decomposition to this step and not bother with in fact adding the terms back up. The one point to adding the terms is to get the numerator and we can obtain that without actually writing down the results of the addition.
At this point we contain one of two ways to proceed. One way will all time work, but is frequently more work. The other, when it won't always work, is frequently quicker when it does work. In this case both will work and thus we'll use the quicker way for this instance.
What we are going to do at this time is to notice that the numerators have to be equal for any x that we would choose to use. Especially the numerators must be equal for plug these in and see what we obtain.
x = -2 5 = A (0) + B (-5) ⇒ B = -1
x = 3 20 = A (5) + B (0) ⇒ A = 4
Thus, by carefully picking the x's we acquire the unknown constants to quickly drop out. Note: These are the values we claimed they would be above.
At this point there really is not a whole lot to do except the integral.
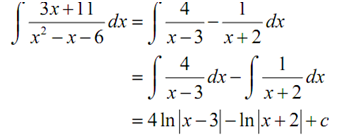
Remind that to do this integral we first split it up into two integrals and after that used the substitutions,
U = x-3
V = x+2
On the integrals to get the last answer